

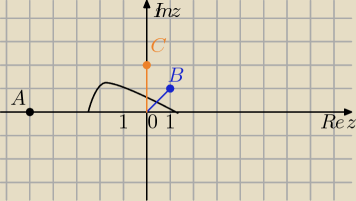
 a) z=−5 punkt A(−5,0)
φ=π
z=5(cosπ+isinπ)
b)z=1+i punkt B=(1;1)
a) z=−5 punkt A(−5,0)
φ=π
z=5(cosπ+isinπ)
b)z=1+i punkt B=(1;1)
| π | ||
φ= | ||
| 4 |
| π | π | |||
z=√2(cos | +isin | ) | ||
| 4 | 4 |
| π | ||
φ= | ||
| 2 |
| π | π | |||
z=2(cos | +isin | ) | ||
| 2 | 2 |
| 8 | 6 | |||
cosφ= | i sinφ= | |||
| 10 | 10 |
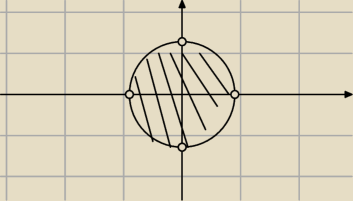 |z|<4
Φ=0 Φ=π
z=2(cos0+isin0)=2 z=2(cosπ+isinπ)=−2
Φ=π/2 Φ=3π/2
z=2(cosπ/2+isinπ/2)=2i z=2(cos3π/2+isin3π/2)=−2i
Ogólnie wynikiem tej nierówności będą liczby zespolone, których moduł jest mniejszy od 4. Na
rysunku tego nie umiem zaznaczyć (nie umiem się posługiwać tym narzędziem). Okrąg powinien być
narysowany linią przerywaną i wnętrze koła powinno być wypełnione. Obliczone punkty nie należą
do rozwiązania, ale należy je obliczyć.
|z|<2 Φ∊(0;π/2)
Φ=0 Φ=π/2
z=√2(cos0+isin0)=√2 z=√2(cosπ/2+isinπ/2)=i√2
Rozwiązanie analogiczne do poprzedniego przykładu z tym, że bierzemy tylko ćwiartkę koła (na
wykresie w ćwiartce 1).
|z|<4
Φ=0 Φ=π
z=2(cos0+isin0)=2 z=2(cosπ+isinπ)=−2
Φ=π/2 Φ=3π/2
z=2(cosπ/2+isinπ/2)=2i z=2(cos3π/2+isin3π/2)=−2i
Ogólnie wynikiem tej nierówności będą liczby zespolone, których moduł jest mniejszy od 4. Na
rysunku tego nie umiem zaznaczyć (nie umiem się posługiwać tym narzędziem). Okrąg powinien być
narysowany linią przerywaną i wnętrze koła powinno być wypełnione. Obliczone punkty nie należą
do rozwiązania, ale należy je obliczyć.
|z|<2 Φ∊(0;π/2)
Φ=0 Φ=π/2
z=√2(cos0+isin0)=√2 z=√2(cosπ/2+isinπ/2)=i√2
Rozwiązanie analogiczne do poprzedniego przykładu z tym, że bierzemy tylko ćwiartkę koła (na
wykresie w ćwiartce 1).
| 3 | ||
y= | ||
| x |
| 3 | ||
x2−( | )2=8 | |
| x |