Proszę o pomoc z kilkoma zadankami
Anka: 1. Dla jakich x∊<−2π;2π> 3tg2x − 1cos2x=5 ?
2. Dany jest prostokąt o bokach 12 i 8. Dłuższy bok zmniejszono o x, a krótszy zwiększono o x.
Wyznacz x tak aby pole kola opisanego na tym prostokącie było największe.
3. Pole trójkąta równoramiennego wpisanego w koło o promieniu 2 wynosi 3√3. Oblicz pole koła
wpisanego w ten Δ.
4. Wyznacz te wartości parametru "p" dla których równanie log(x−p)(2x−p)=2 ma dokładnie
dwa różne pierwiastki ujemne.
Bardzo dziękuję!
Ania
26 gru 20:16
think: ad 1)
3sin
2x − 1 = 5cos
2x
3sin
2x − 1 = 5(1 − sin
2x)
8sin
2x = 6
| | √3 | | √3 | |
sinx = |
| ⋁ sinx = − |
| |
| | 2 | | 2 | |
| | π | | 2π | | −π | | −2π | | −5π | |
x = |
| lub x = |
| lub x = |
| lub x = |
| lub x = |
| lub x = |
| | 3 | | 3 | | 3 | | 3 | | 3 | |
| | −4π | | 4π | | 5π | |
|
| lub x = |
| lub x = |
| |
| | 3 | | 3 | | 3 | |
26 gru 22:52
think: ad 2) aby pole było największe, to i przekątna prostokąta musi być jak najdłuższa
czyli chodzi o maksymalizację funkcji
√(12 − x)2 + (8 + x)2
x∊<0, 12) ponieważ chcemy aby to był prostokąt nie odcinek, więc nie możemy odjąć więcej niż 12
skupimy się tylko na wartości pod pierwiastkiem
x2 − 24x + 144 + x2 + 16x + 64 → max na przedziale <0,12)
2x2 − 8x + 208
xw = 2 czyli największą wartość na przedziale <0,12) funkcja osiągnie gdy x→12
26 gru 22:56
edi:
3/ było ok

26 gru 23:03
think: edi nie było bo to jest trójkąt równoramienny a nie równoboczny
26 gru 23:04
think: ad 3) niestety nie mam pomysłu jak to zrobić
26 gru 23:13
think: podejrzewam, że przydałby się wniosek albo twierdzenie, że spośród trójkątów wpisanych w okręg
największe pole ma trójkąt równoboczny, a to podane pole jest akurat maksymalne... ale nie
znam takiego twierdzenia.
26 gru 23:28
edi:
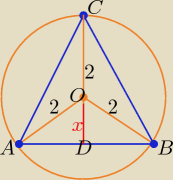
|AB|= 2
√4−x2 , x∊(0,2) , |CD|= 2+x
P=(2+x)*
√4−x2= 3
√3 /
2
(4−x
2)(2+x)
2=27 ⇒ x=1
|CD|= 3 , |BC|=|AC|= 3
√2 i |AB|= 2
√4−1= 2
√3
trójkąt ABC jest równoboczny o boku długości
2√3
r
w= 1 P(koła wpisanego)= π
26 gru 23:44
edi:


26 gru 23:45
think: 
dzięki Edi

27 gru 16:35
edi:

27 gru 16:49

 |AB|= 2√4−x2 , x∊(0,2) , |CD|= 2+x
P=(2+x)*√4−x2= 3√3 /2
(4−x2)(2+x)2=27 ⇒ x=1
|CD|= 3 , |BC|=|AC|= 3√2 i |AB|= 2√4−1= 2√3
trójkąt ABC jest równoboczny o boku długości 2√3
rw= 1 P(koła wpisanego)= π
|AB|= 2√4−x2 , x∊(0,2) , |CD|= 2+x
P=(2+x)*√4−x2= 3√3 /2
(4−x2)(2+x)2=27 ⇒ x=1
|CD|= 3 , |BC|=|AC|= 3√2 i |AB|= 2√4−1= 2√3
trójkąt ABC jest równoboczny o boku długości 2√3
rw= 1 P(koła wpisanego)= π


 dzięki Edi
dzięki Edi 
