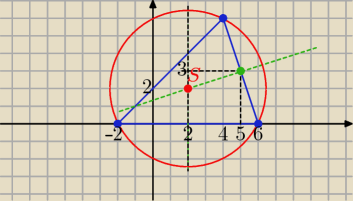
pytanko matematyczne - wyznacz srodek okregu xartez: wyznacz wspolrzedne srodka okregu opisanego na trojkacie o wierzcholkach a(−2,0) b(6,0) c (4,6) mam pytanko do tego zadania, obliczylem to z punktu przeciecia prostych zawierajacych srodki BC i AC i odpowiednio wierzcholkow A i B po wszystkich obliczeniach wyszly mi wspolrzedne

	8
S(		,2) to samo wychodzi jakby podstawic dane do wzoru na srodek ciezkosci trojkata. Czy
	3

to wyjatkowy przypadek, czy tez mozna to zastosowac w kazdym zadaniu tego typu?

Bogdan: Wyznacz jeszcze raz współrzędne środka tego okręgu, powinno wyjść: S = (2, 2)

edi:

xartez: moje rozumowanie bylo delikatnie mowiac mylne.. rozwiazalem inaczej wyszlo prawidlowo. dzieki

Aga1.: Środek ciężkości trójkąta to punkt przecięcia się środkowych, a środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych boków. Punkty te pokrywają się w trójkącie równobocznym.