praca kontrolna alusia: Znajdz obrazy punktow A(1;2) B(−5;−2) C(−3;3) w przesunieciu o wektor v=[2;−2] Przedstaw w ukladzie XOY Prosze o pomoc

alusia: oblicz boki i katy trojkata w ktorym a=8 c=16 ∡β=60

alusia: dla jakich wartosci x w podanej kolejnosci tworza ciag arytmetyczny: 7+x ; 9+2x ; 11+3x

Mateusz: 1) Punkt np A=(x,y) przesunięty o wektor v=[a,b] daje ci punkt np B ktorego wspołrzedne wynoszą: B=(x+a,y+b) 2) Geometria nie chce mi sie robic

	an−1+an+1
3) Skorzystaj z własnosci: an=
	2

Dominik: 2) twierdzenie cosinusow sie klania

Janek 191: z.1 A = ( 1;2), B = ( −5; −2), C = (−3; 3) −> v = [ 2 ; − 2] zatem A' = ( 1 + 2; 2 + (−2)) = ( 3; 0) B' = ( − 5 + 2; − 2 + (−2)) = ( − 3; − 4) C' = ( − 3 + 2; 3 + (−2)) = ( − 1; 1 ) ============================== Jeżeli A = ( x; y) −> v = [ a ; b ], to A' = ( x + a; y + b) ================================ z.2 a = 8 , c = 16 β = 60 zatem α = 90 − 60 = 30 Z tw. Pitagorasa mamy a² + b² = c² => b² = c² − a² = 16² − 8² = 256 − 64 = 192 = 64*3 więc b = √64*3 = √64 *√3 = 8 √3 ================================== z.3 a2 −a1 = a3 − a2 więc ( 9 +2x) − ( 7 +x) = (11 +3x) − ( 9 +2x) 2 + x = 2 + x x może być dowolną liczbą rzeczywistą. ====================================

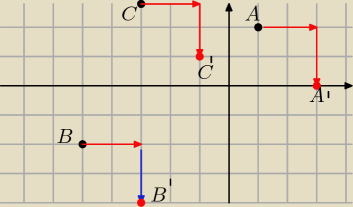
Aga1.: W układzie współrzędnych bez obliczeń ( zaznaczasz punkt np. A i przesuwasz go o 2 jednostki w prawo, a następnie o 2 jednostki w dół, bo masz wektor przesunięcia [2,−2])

Aga1.: W zadaniu 2) nie jest napisane, że trójkąt jest prostokątny (nie można z góry zakładać), chociaż z obliczeń tak wyjdzie.

alusia: dziekuje bardzo mam jeszcze zadanko oblicz wartosc iloczynu skalarnego wektorow a, b jezeli v [a]=8 , v [b]=6 ∡(va, vb)= 30

alusia: okrag o srodku S(2;−5) i promieniu r=3 jakim jest opisany rownaniem

alusia: punkty A(2;−3) B(5;1) sa wierzcholkami kwadratu ABCD. jaka ma dlugosc przekatna tego kwadratu

slaby: 1) → → → → → → a □ b = |a| * |b| * cos(a,b) = 8 * 6 * cos30= 12√3 2) (x−2)² + (y+5)²=9 3) |AB|=√(5−2)² + (1+3)²= √9+16=5 |AC|=√2|AB|=5√2

alusia: a na te pierwsz zadanie to jakie sa dokladnie wzory? dlaczego z cos30

Janek 191: Iloczyn skalarny wektorów : → → a □ b = a * b* cos 30 = 8*6 * √3/2 = 24 √3

Janek 191: z.2 a = 8, c = 16, β = 60 Z tw. cosinusów mamy: b² = a² + c² − 2 ac*cos β b² = 8²+ 16² − 2*8*16* cos 60 = 64 + 256 − 256*(1/2) = 320 − 128 = 192 = 64*3 więc b = √64*3 = √64* √3 = 8 √3 Sprawdzam czy trójkąt jest prostokątny ? 8 < 8 √3 < 16 zatem 8² + ( 8 √3 )² = 64 + 192 = 256 = 16² Tak, zatem α = 90 − β = 90 − 60 = 30 oraz γ = 90 ===============================================