? Patryk: |x−|x−3||<4 x−|x−3<4 ∧ x−|x−3>−4

	1
x∊R ∧ x>−
	2

	1
x∊(−		;∞)
	2

dobzre ?

Tad: ... nie dobrze −

Patryk: ok i tak nie zrozumiem

Basiek: Rozwiązanie do przeanalizowania: x−|x−3|<4 ∧ x−|x−3|>−4 |x−3|>x−4 ∧ |x−3|<x+4 (i teraz każde z tych dwóch będzie rozwiązywane ... jakby osobno) (x−3>x−4 ⋁ x−3<−x+4) ∧ (x−3<x+4 ∧ x−3>−x−4) I tu już zapewne sobie poradzisz... PS. Mam nadzieję, ze nic nie pomyliłam.

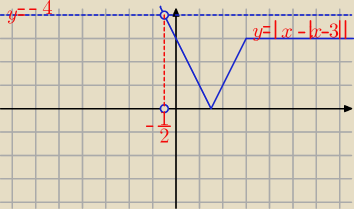
Bogdan: czy widać rozwiązanie?

Patryk: takie jak przedstawiłem na początku

Bogdan: tak

Patryk: (x−3>x−4 ⋁ x−3<−x+4) ∧ (x−3<x+4 ∧ x−3>−x−4) czy to na pewno jest ok ?

Patryk: Basiek

ZKS: Dobrze Basiek Ci napisała.

Patryk: np rozwiazaniem tego |x−3|>x−4 jest zbiór liczb rzeczywistych (x−3>x−4 ⋁ x−3<−x+4)

	7
−3>−4 ∨ x<
	2

jakoś nie bardzo wychodzi

ZKS: I z tego dostajesz zbiór liczb rzeczywistych dokładnie ale masz jeszcze drugi człon i (x − 3 < x + 4 ∧ x − 3> −x − 4).

Patryk: ok już widze,dzięki

ZKS: Na zdrowie.