? Patryk: dla jakich wartości parametru m równanie sin²x+sinx+m=0 ma rozwiązania ? t=sinx Δ≥0 to chyba za mało ?

ICSP: za mało

Patryk: co jeszcze ?

Saizou : a jakie wartości przyjmuje sinx

Patryk: <−1;1>

Patryk:

	1
czyli <−1;		> ?
	4

Maslanek: To też mało 0≤sin²x+sinx≤2

Maslanek: 1−4m≥0

	1
m≤
	4

Więc właściwie m∊<−2,0>.

Patryk: skąd ci się to wzięło ? Maslanek

Maslanek: Kurde To też za mało Warunki: m∊<−2,0) − żeby równanie miało sens... Δ≥0 t₁, t₂∊<−1,1> Taki układ nierówności do rozwiązania. U mnie nie ma ostatniego jeszcze. Także to jest źle póki co

Maslanek: Z zerem oczywiście m−y

Patryk: znalazłem inny sposób,ale dzięki

Maslanek: To przedstaw

Maslanek:

	1		1
Czyżby (sinx+		)2−		+m=0
	2		4

	1		1
(sinx+		)2=		−m.
	2		4

	1
m≤		− sens liczbowy
	4

m≥−2? − najwyższa wartość kwadratu

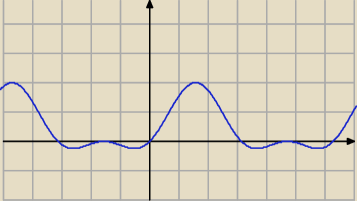
aniabb: sin²x +sinx=−m m∊<−2;1/4>

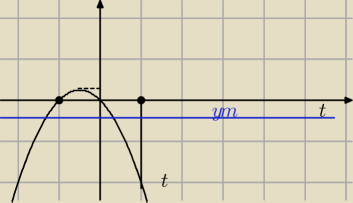
Patryk: −t²−t=m na podstawie wykresu

Patryk:

	π
czy cosx+√3sinx to sin(		+x) ?
	6

Patryk: a jednak nie, dobra już wiem

Mila: sin²x+sinx+m=0 t²+t=−m i t∊<−1;1> t(t+1)=−m

	−1
tw=		∊<−1;1>
	2

	1		−1
f(−		)=		najmniejsza wartość funkcji f(t)=t2+t w przedziale <−1;1>
	2		4

Szukamy największej wartości f(−1)=0 f(1)=2

	−1		1
−m≥		⇔m≤
	4		4

i −m≤2⇔m≥−2 odp:

	1
m∊<−2;		>
	4

Masz to samo z Twojego wykresu.