Mając bok większego kwadratu oblicz bok mniejszego, tak by wierz... Trix: Mając bok większego kwadratu oblicz bok mniejszego, tak by wierzchołki mniejszego kwadratu były zawarte w boku większego kwadratu. (kwadrat wpisany w kwadrat). Mniejszy kwadrat jest obrócony o dowolny kąt α. Z góry piszę, że równania z dwoma i z większą ilością niewiadomych odpada, ponieważ chcę to zastosować w praktyce(piszę program generujący tzw. wirujące kwadraty)

Trix:

Ajtek: Tw. Pitagorasa i jedziesz.

aniabb: bok mniejszego b=√2x²−2ax+a² x∊(0;a)

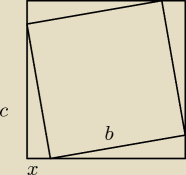
Trix: No dobra ale nie znam x, znam tylko kąt i bok większego kwadratu, z x'em to nie wypali, ponieważ pojawiłyby się jeszcze więcej równań. Dal kolejnych odwiedzających narysuję co według UP jest x, a i b (a=x+c)

aniabb: za x wstaw bsinα (2sin²α−1)b² −2asinα b +a² Δ = 4a²sin²α − 8a²sin²α + 4a² = − 4a²sin²α + 4a² = 4a²cos²α √Δ = 2acosα

	2asinα+2acosα
b=
	2(2sin2α−1)

aniabb: wróć..mianownik jest ujemny więc wybieramy drugie b ( z minusem) czyli b= a(sinα−cosα)/(−cos2α)

aniabb: albo jeszcze upraszczając

	a
b=
	sinα+cosα