| 3n + cosn | ||
an = | ||
| 4n − 1 |
| 1 | ||
3n − 1 ≤ 3n + cosn < 3n + 1 // * | ||
| 4n −1 |
| 3n − 1 | 3n + cosn | 3n + 1 | |||
≤ | ≤ | ||||
| 4n −1 | 4n − 1 | 4n − 1 |
| 3 | ||||||||||||
lim | = ( | )n = 0 | |||||||||||
| 4 |
 dzięki.
n√4n − cosn
−1≤cosn≤1
4n−1≤4n + cosn≤4n+1
n√4n −1 ≤n√4n + cosn ≤ n√4n+1
n√4n −1 = 4n√1 = 4, góra też do 4, an → 4
i takie pytanie:
n√an = a
n√an + 4 = a*n√4, ale n√4 → 1 tak? to tak samo działa jak logarytm:
jęzeli logab, gdzie b > 1 to to dla dowolnego a (uwzgledniajac dziedzine) on nigdy nie będzie
mniejszy od 1?
dzięki.
n√4n − cosn
−1≤cosn≤1
4n−1≤4n + cosn≤4n+1
n√4n −1 ≤n√4n + cosn ≤ n√4n+1
n√4n −1 = 4n√1 = 4, góra też do 4, an → 4
i takie pytanie:
n√an = a
n√an + 4 = a*n√4, ale n√4 → 1 tak? to tak samo działa jak logarytm:
jęzeli logab, gdzie b > 1 to to dla dowolnego a (uwzgledniajac dziedzine) on nigdy nie będzie
mniejszy od 1?
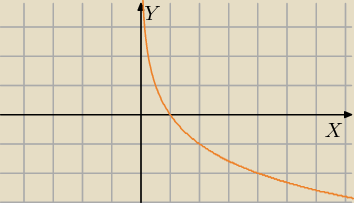 n√c→1 c −stała ( c≠0)
Granica dobrze, ale to o logarytmie nie
a∊(0;1)
y=ln1/2(x)
n√c→1 c −stała ( c≠0)
Granica dobrze, ale to o logarytmie nie
a∊(0;1)
y=ln1/2(x)
| |||||||||||||||||||||||
lim = | =.. | ||||||||||||||||||||||
|
| 1 − (1/4)n | ||
Sn = | ||
| 3/4 |
| 1 − (1/3)n | ||
Sn = | = | |
| 2/3 |
|
| ||||||||||||||
= | = | ||||||||||||||
|
|
| 1 | 4 | |||
odwróciłem ( | = | ) | ||
| 3/4 | 3 |
| 4 | 2 | 8 | 9 | ||||
* | = | . W odpowiedziach jest | , gdzie ten babol? | ||||
| 3 | 3 | 9 | 8 |
| 3/4 | 3*3 | 9 | |||
= | = | ||||
| 2/3 | 4*2 | 8 |