... xylofon: Na ile sposobów możemy sposrod liczb 1,2,3,...,2n−1,2n wybrac pare liczb (x, y) takich, że iloraz x i y należy do przedziału (1,2]?

xylofon: podbijam

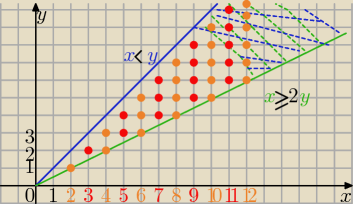
Eta: Ja rozwiązałabym to zadanie tak: ( z wykorzystaniem rys.) Zd. A −−− takie ,że (x,y)€ {1,2,3,....., 2n−1, 2n}, n€ N+

	x
i takie,że 1<		≤2
	y

Zatem takie pary muszą spełniać układ nierówności x <y i x ≥ 2y czyli są to pary punktów (pomarańczowe i czerwone w części płaszczyzny zaznaczonej na rys) Liczb parzystych w tym zbiorze jest n i nieparzystych też n Zb.A₁ −−− wyznaczamy ilość takich par dla n −− parzystych A₁= {(2,1) (4,2) , (4,3), (6,3), (6,4), (6,5) ...........}

	n(n+1)
ilość takich par jest : 1+2+3+.... +n =		−−− suma ciągu arytm.
	2

Zb. A₂ −−−− ilość takich par dla n −− nieparzystych ( bez 1) A₂={ (3,2), (5,3), (5,4), (7,4), (7,5), (7,6).......}

	(n−1)(n−1+1)		(n−1)*n
ilość takich par: 1+2+3+... + (n−1) =		=
	2		2

Zatem |A|= |A₁|+|A₂| = ............ = n² może jeszcze ktoś poda Ci inny sposób

aniabb: bardzo fajny uwielbiam sposoby graficzne

Eta: