prosze o pomoc asdf: Witam mam problem z dwoma zadaniami bardzo proszę o pomoc w ich rozwiązaniu mianowicie : zad 1 Wiedząc że przedział (−³₂ ; 0) jest zbiorem wszystkich rozwiązań nierówności ²_x < m z niewiadomą x , oblicz m zad 2 Dane jest równanie x² + bx + c = 0 z niewiadomą x , Wyznacz wartości b i c tak by były one rozwiązaniami danego równania

Artur_z_miasta_Neptuna: b i c rozwiązaniami a więc: b*c = c ⋀ b+c = b <−−−wzory Viete'a b=1 ⋀ c=0 tara

Artur_z_miasta_Neptuna: znaczy się b=1 ⋀ c≠0 => sprzeczne b∊R ⋀ c=0 −−− si

PW:

2		2		2−mx
	<m ⇔		−m <0 ⇔		<0 ⇔ x(2−mx) < 0 (iloraz ma taki sam znak jak iloczyn)
x		x		x

	2
−x(mx−2)<0 ⇔ −mx(x−		) <0. Można było podzielić przez m, gdyż m≠0 − wynika to z treści
	m

zadania, bo zbiór wszystkich rozwiązań nierówności

	2
		<0
	x

	3
nie jest przedziałem (−		, 0).
	2

Nierówność

	2
−mx(x−		) <0
	m

rozwiązać biorąc pod uwagę dwa przypadki: dla m<o i dla m>0 − różne zwroty nierówności po podzieleniu stronami przez (−m) − i porównać z rozwiązaniem narzuconym w treści zadania.

asdf: Artur nie rozumiem dlaczego tak poprawiłeś ?

b.: 2. 2b² + c = 0 c² + bc + c =0 odejmujemy stronami: 2b² − c² − bc = 0 (b−c)(b+c) + b(b−c) = 0 (2b+c)(b−c) = 0 stąd c=b lub c=−2b 1. gdy c=b, wstawiamy 2b² + b = 0 b(2b+1) = 0 czyli b=c=0 lub b=c=−1/2 2. gdy c=−2b: 2b² − 2b = 0 b(b−1) = 0 czyli b=c=0 lub b=1, c=−2 ostatecznie dostajemy trzy pary rozwiązań @Artur: 1. masz błąd we wzorach Viete'a − brakuje minusa 2. b i c są rozwiązaniami, ale niekoniecznie różnymi, co wyklucza użycie wzorów Viete'a

asdf: a można by naprzykład zrobić tak że jak to już PW przekształcił czyli −mx² + 2x <0 a wiemy z treści że x należy ( −3/2 ; 0) więc −³₂ i 0 są miejscami zerowymi i wiemy że parabola musi być taka wówczas jak wyżej więc wiadomo że m<0 żeby współczynnik był dodatni czy to jest dobre rozwiązanie?

Artur_z_miasta_Neptuna: asdf ... poprawilem ... bo w pierwszym równaniu dzieliłem przez c ... więc c≠0 i drugie równanie sprzeczne. drugi przypadek dla c=0 ... oba równania spełnione dla dowolnego x

PW: @asdf: masz racje, nie trzeba się nad tym m tak rozwodzić "na przypadki" − skoro rozwiązaniem nierówności f(x) <0 jest przedział, to funkcja kwadratowa musi osiągać minimum ("ramiona w górę"). Czysta przyjemność pomagać myślącemu.

Mila:

	2
1)f(x)=
	x

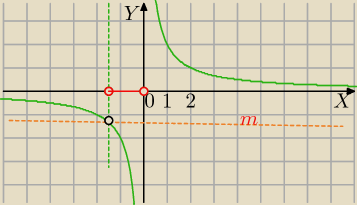
	−3		−3		−2		−4
f(		)=U{2:		)=2*		=
	2		2		3		3

I sposób

	−4
odczytuję z wykresu, że dla x∊(−U{3}[2};0) wykres funkcji f(x) leży poniżej prostej y=
	3

	−4		2		−4
⇔m=		⇔		<
	3		x		3

II sposób algebraicznie

	−3
x>		i x<0
	2

	−3
x>		/:x (przy podanych założeniach)
	2

	−3		−2
1<		/*
	2x		3

−2		1
	>		/*2
3		x

−4		2
	>		⇔
3		x

2		4		4
	<−		⇔m=−
x		3		3

Mila: 2) Skorzystaj z równości: (x−b)(x−c)=x²+bx+c utwórz układ z porównania współczynników b=0 i c=0 ( wtedy mamy x²=0 i zgadza się lub dla c≠0 b=1 i c=−2 (wtedy x²+x−2=0) sprawdź rozwiązania