Rozwiąż graficznie równiania: vanillia: rozwiąż graficznie równiania: a) 2^x+3= −x

	1		3
b) (		)x+		=0
	3		x

	3		1
c) −2x−1=−		x+
	2		2

	1
d) I(		)x−1I=−2x2−8x−5
	2

	1
e) 2−(		)x=Ix+1I
	2

f) 3^x−1=−2x²+4x

vanillia: wgl od czego zacząć?

Tad: przykład a) Po lewej stronie funkcja wykładnicza ... wykres znasz ... (f(x)=2^x ... przesunięte ...) Po prawej stronie prosta f(x)=−x Rysuj i zaznacz punkt przecięcia ...

PW: a) To proste: znany z lekcji wykres funkcji f(x) = 2^x przesunąć o wektor [−3,0] − dostaniemy wykres funkcji g(x)=f(x+3)=2^x+3. W tym samym układzie współrzędnych narysować wykres funkcji h(x) = −x i zobaczyć, gdzie przecinają się wykresy g(x) i h(x). Odcięte ("x−owe współrzędne") tych punktów wspólnych to pierwiastki równania − odpowiadają na pytanie "dla jakich x jest 2^x+3 = −x". Wszystkie zadania polegają na tym samym: przypomnieć jak wyglądają wykresy występujących tam funkcji i zobaczyć gdzie przecinają się.

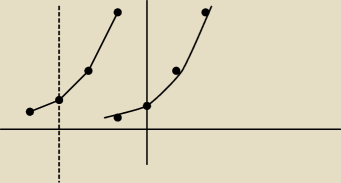
vanillia: ok, po lewej stronie wykres jest przesunięty o 3 miejsca w lewo

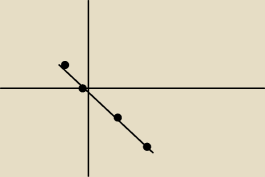
vanillia: ten drugi taki

PW: Ale w jednym układzie współrzędnych, żeby zobaczyć punkty wspólne wykresów.

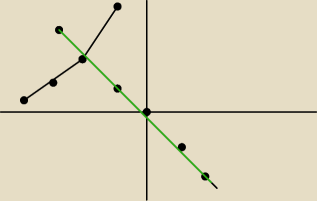
vanillia: to ma wyglądac tak? wiec punkt wspolny to (−2,2)

vanillia: a jak mam wartość bezwzględną to mam rozpatrywać dwa przypadki?

PW: No pięknie, autor zadania był łaskawy i dał takie rozwiązanie, które po odczytaniu z wykresu sprawdza się dokładnie z rozwiązaniem rzeczywistym: odczytaliśmy, że x=−2 i rzeczywiście 2⁻²⁺³ = −(−2). Gdy jest wartość bezwzględna, to nie tyle dwa przypadki, co − dokładniej mówiąc − po narysowaniu wykresu funkcji "bez kresek" zastosować symetrię względem osi Ox tej części wykresu, która leży pod osią. Tam, gdzie wartość funkcji f jest dodatnia lub zero, to |f(x)| = f(x). Wartość bezwzględna jest bezradna wobec dodatnich − zostawia ich w spokoju. Jest natomiast bezwzględna dla ujemnych − zamienia ich na dodatnich, czyli zmienia im znak. Taka zmiana wartości funkcji z ujemnej na dodatnią to właśnie symetria względem osi Ox (z dołu do góry). Przepraszam, że tak tłumaczę "jak chłop krowie", ale nie wiem, z czym masz kłopot, może nie trzeba aż tak?

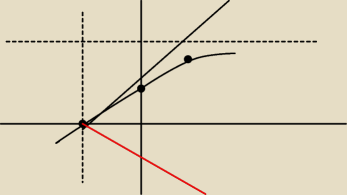
vanillia: do podpunktu e) oki tak rozkminiam to i srednio mi to wychodzi. narysowałam i wychodzi mi cos takiego. to jest dobrze to na czerwono to odbicie tej wartosci bezwzglednej