Trygonometria Cinia: Udowodnij, że nierówność sinα + cosα > 1 jest prawdziwa dla każdego kąta ostrego α.

Godzio:

	√2		√2		π		π
sinα + cosα = √2(		sinα +		cosα) = √2(cos		sinα + sin		cosα) =
	2		2		4		4

	π
= √2sin(		+α)
	4

	π
Teraz zauważmy, że skoro α jest kątem ostrym to, 0 < α <
	2

	π		π
√2sin(		+α) > √2sin		= 1
	4		4

	π		π		π		π
√2sin(		+		) < √2sin(		+α) ≤ √2sin(		) = √2
	4		2		4		2

	π		π
L = √2cos		= 1 zatem √2sin(		+α) > 1
	4		4

	π
Po co sprawdzałem drugie ? Bo jeżeli weźmiemy α =		to sinus przeskakuje swoją największą
	2

wartość i zaczyna maleć, pokazaliśmy, że w tym przedziale nie zmaleje poniżej 1

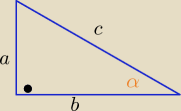
Eta: Dla kąta ostrego α a>0 , b>0 , c>0 i z nierówności trójkąta a+b >c

	a		b
sinα=		, cosα=
	c		c

	a		b
to:		+		>1 /*c
	c		c

a+b>c .. zachodzi c.n.u

Eta: Co Godzio na to?

pigor: ... , jeśli α − ostry, to sinα+cosα>1 ⇒ (sinα+cosα)²>1² ⇒ 1+2sinαcosα>1 ⇒ sinα sinα>0 c.b.d.u. ...

pigor: ... oczywiście ... miało być na końcu sinα cosα >0 .

pigor: co jest prawdą dla ∀α ostrego

Eta:

PW: @Eta, ja też jestem zdania, że dowody elementarne są najpiękniejsze (nie strzelać z armaty do muchy, jak mawiają wojskowi entomolodzy). Ciekawe, jak policzą sin²37°+sin²53°.

Eta: Myślę,że zauważą 37^o+53^o= 90^o i po bólu Pozdrawiam PW i tradycyjnie ....