Zadania z urną i kulami calc: 1.W urnie jest 8 kul białych i n czarnych. Z tej urny wyjmujemy dwie kule, odkładamy na bok i z pozostałych kul losujemy jedną. Prawdopodobieństwo wylosowania teraz z tej urny kuli białej jest większe od ³₄. Wyznacz liczbę n. 2.W pierwszej urnie jest 6 kul białych i 4 czarne, a w drugiej − cztery białe i n czarnych. Z pierwszej urny przekładamy jedną kulę do drugiej urny. Z drugiej urny wyjmujemy teraz dwie kule. Prawdopodobieństwo wylosowania z drugiej urny pary kul różnokolorowych jest większe od ²₅. Wyznacz wszystkie możliwe wartości liczby n. Próbowałem zrobić te zadania za pomocą drzewa, jednak nie bardzo wiem jak.

Artur_z_miasta_Neptuna:

	8*7*6		n*8*7		n*(n−1)*8
P(A) =		+		*2 +
	(n+8)(n+7)(n+6)		(n+8)(n+7)(n+6)		(n+8)(n+7)(n+6)

	3
P(A) >
	4

wyznacz 'n'

calc: ok, ale skąd się to wzięło? da się to zadanie rozrysować na drzewie?

Artur_z_miasta_Neptuna: da się ... oczywiście że się da ... wszystko co można zapisać w postaci ułamka da się rozpisać na drzewku ... tyle że trzeba mieć dużą kartkę i wyjdzie Ci dokładnie to co napisałem tam

calc: rozwiązanie jest dobre, jednak nie wiem skąd się wzięło wszystko pokolei, a chciałbym zrozumieć to zadanie i umieć rozwiązać podobne, np. drugie

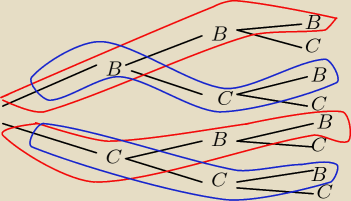
Artur_z_miasta_Neptuna: kolorami zaznaczyłem to co Ciebie interesuje ... wpisz prawodpodobieństwa ... nie pisałem bo jest to uciążliwe i by już nic nie było widać

calc: okej, zrozumiałem to zadanie i udało mi się dzięki temu zrobić drugie samemu, dzięki wielkie!

ulysses: Czy ktos posiada odpowiedz do tego zadania?