ostroslup
Mat: Podstawą ostrosłupa jest trójkąt prostokątny równoramienny, którego przyprostokątna ma 4cm.
Wszystkie krawędzie boczne maja jednakową długość, równą
√33 cm. Oblicz:
a. wysokość .
b. sinus kata nachylenia ściany bocznej o mniejszym polu do płaszczyzny podstawy.
wysokość mi wychodzi 5 , podpunkt b mnie intesesuje
19 gru 18:28
Mat: ?
19 gru 19:24
dero2005:
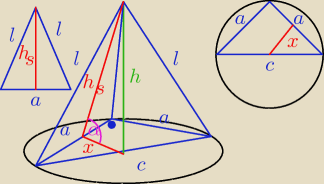
a = 4
l =
√33
c = a
√2 = 4
√2
h = p{l
2 − (
c2)2 = 5
h
s =
√l2 − (a2)2 =
√29
| | h | | 5 | | 5√29 | |
sin α = |
| = |
| = |
| |
| | hs | | √29 | | 29 | |
19 gru 20:05
dero2005:
h = √l2 − (c2)2 = 5
19 gru 20:06
Mat: Dzięki...z czego liczyłeś h ściany ?
19 gru 20:20
Mat: aaa to
√332 − 2
2 .... Dzięki bardzo
19 gru 20:22
dero2005:
Ponieważ wszystkie krawędzie boczne mają jednakową długość to ściana boczna jest trójkątem
równoramiennym o podstawie a i ramionach l (rysunek po lewej stronie) więc wysokość liczymy z
Pitagorasa
19 gru 20:26
Mat: A spodek wysokości mógłby być np. w środku okregu wpisanego w dowolny trojkąt prostokątny , o
roznych dlugosciach krawedzi bocznych ? Czy jedynie może być w wierzcholku kąta prostego i na
polowie przekątnej podstawy ? Potrafisz mi wyjasnic ?
19 gru 20:30
Mat: ehh szkoda ...
19 gru 20:50
dero2005:
Jeżeli w zadaniu jest napisane, że ściany boczne są pochylone do podstawy pod jednakowym kątem
to spodek wysokości leży w środku okręgu wpisanego w trójkat podstawy i tutaj krawędzie boczne
śą różnej wielkości
Jeżeli jest napisane, że krawędzie boczne są pochylone pod jednakowym kątem do podstawy to
spodek wysokości leży w środku okręgu opisanego na trójkącie podstawy
Jeżeli podstawa jest trójkątem prostokątnym to spodek wysokości leży na połowie
przciwprostokątnej(ten przypadek), krawędzie boczne są jednakowej długości
19 gru 20:59