19 gru 17:40
snake: hm?
19 gru 18:27
Artur_z_miasta_Neptuna:
8.
sposób I
| | a√2 | |
przekrój lewy to trapez o podstawach a√2 i |
| |
| | 2 | |
| | a√2 | |
przekrój prawy to trójkąt o podstawie |
| |
| | 2 | |
obie figury mają jednakową wysokość
stąd:
| P1 | | | | 1.5a√5 | |
| = |
| = |
| = ... |
| P2 | | | | 0.5a√2 | |
stąd stosunek pól wynosi
jest jeszcze (przynajmniej) jedno inne rozwiązanie, która jest szybsze i bardziej hmmm
pomysłowe
19 gru 18:40
Artur_z_miasta_Neptuna:
7. a narysuj ten ostrosłup
19 gru 18:41
snake:
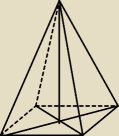
19 gru 18:49
snake: Podstawa to kwadrat o długości a=2. Ściany boczne to trójkąty równoramienne. Krawędź boczna
3√2.
19 gru 18:50
Tad:
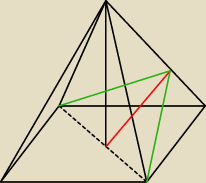
Zad.1
Szukasz trójkąta który w podstawie ma a
√2 ... a najmniejsze pole ... przy najmniejszej
wysokości ... czyli prostopadłej do krawędzi ...
19 gru 18:56
Tad:
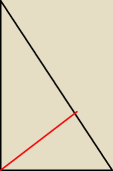
..skorzystaj z podobieństwa trójkątów
19 gru 18:58
Artur_z_miasta_Neptuna:
zauważ ... że skoro przekrój zawiera przekątną podstawy ... to ów przekrój będzie miał kształt
trójkąta ... o podstawie równej przekątnej podstawy tegoż ostrosłupa ... tak więc ... pole
przekroju zależeć będzie tylko od wysokości tegoż trójkąta.
A czymże będzie wysokość
wysokość będzie odległością pomiędzy krawędzią (przez którą
przechodzi przekrój) a środkiem podstawy ostrosłupa
A jaka jest najmniejsza odległość punktu (środek podstawy ostrosłupa) od prostej (krawędź
boczna)
Oczywiście najmniejsza odległość będzie pod kątem prostym do tejże prostej ...
czyli będzie to wysokość trójkąta zbudowanego z:
− krawędzi bocznej
− wysokości ostrosłupa
− połowy przekątnej podstawy
oblicz pole tego trójkąta ... wyznacz wtedy h dla podstawy będącej krawędzią ostrosłupa ... i
już masz wszystkie dane aby obliczyć najmniejsze możliwe pole przekroju
wszystko jasne
19 gru 19:00
snake: Dalej wszystko jasne raczej, tylko z tym podobieństwem trójkątów nie za bardzo rozumiem.
19 gru 19:10
Artur_z_miasta_Neptuna:
masz podobieństwo kąt,kąt,kąt (jeden wspólny ... oba trójkąty mają kąt prosty ... więc trzeci
też musi być taki sam)
19 gru 19:11
snake: A wysokość tego przekroju jest oparta na krawędzi ostrosłupa i dzieli ją na 2/3 i 1/3?
19 gru 19:26
Artur_z_miasta_Neptuna:
snake ... szczerze −−− to nie wiem ... może ... zależy od wymiarów ostrosłupa
19 gru 19:57
snake: Ech, no to nie rozumiem dalej... Mógłbyś rozpisać tą kwestię z podobieństwem trójkątów?
19 gru 20:07
Artur_z_miasta_Neptuna:
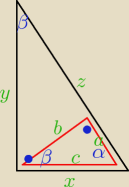
19 gru 20:10
snake: według moich obliczeń wyszło tak:
x=√2
y=4
z=3√2
a=4√23
b=43
c=√2
tylko nie wiem dalej do czego te wszystkie dane się przydadzą..
19 gru 20:41
snake: okej, już mi się udało. dziękuję bardzo za pomoc i cierpliwość
oba wyniki wyszły zgodnie z
odpowiedziami, pozdrawiam
19 gru 22:30
