funkcje
RATUNKU!!!!: Dziedziną funkcji opisanej wzorem f(x)=√x2 − 2√2x + 2 jest zbiór:
A {1;2;3;4;5;6;}
B R − {4}
C <−2;∞)
D R
Prosze nie tylko o sama odpowiedz ale rowniez o rozwiazanie
19 gru 16:16
123_123_123_123: Wyrażenie pod pierwiastkiem wieksze od zera
19 gru 16:18
Artur_z_miasta_Neptuna:
wieksze równe
19 gru 16:19
RATUNKU!!!!: a czy moge prosic o rozwiazanie
bo jaka zasada jest to wiem... ale zawislem w pewnym etapie i
ni jak nie moge ruszyc
19 gru 16:21
Artur_z_miasta_Neptuna:
rozwiąż:
x2 − 2√2x + 2 > 0
to będziesz miał wynik ... podpowiem ... to na pewno nie będzie odpowiedź A
19 gru 16:22
123_123_123_123:
Sorry, ≥ 0
x
2 − 2
√2x + 2 ≥ 0
Δ = 0
x∊R
19 gru 16:22
Artur_z_miasta_Neptuna:
tfu tfu oczywście
≥ ma być
19 gru 16:24
RATUNKU!!!!: ooo dziekuje... probowalem troche inaczej do tego podejsc i poprostu wyliczyc x a wygladalo to
mw. tak:
x
2−2
√x+2≥0
x
2≥−2+2
√x
x
2≥2(−1+
√x) /*(−1+
√x)
x
2*(−1+
√x)≥2
no i tu zawislem
19 gru 16:26
123_123_123_123: No to nie za dobrze
To proste równanie kwadratowe, a tak btw. to skad w 3 linijce wzielo sie / * (−1+√x) ?
19 gru 16:28
RATUNKU!!!!: a przepraszam moj blad... x nie bylo pod √ i je niepotrzebnie tam upchnolem
19 gru 16:28
123_123_123_123: Chodziło mi o mnożenie
Jak masz x
2 ≥ 2(−1+
√x) i to pomnożysz przez (−1+
√x) to masz
x
2(−1+
√x) ≥ 2(−1+
√x)
2
19 gru 16:31
RATUNKU!!!!: tak tak... teo tez juz zauwazyle
ale niestety twojego rozwiazania tez nie ma w odpowiedziach
19 gru 16:34
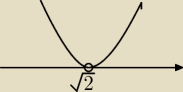
123_123_123_123: Jest bo masz jedno miejsce zerowe x
0=
√2 a miałeś ≥ 0, więc rozwiązaniem jest wszystko co
lezy na osi x lub nad osią, z wykresu widać, że jest to zbiór R
x∊R
19 gru 16:35
RATUNKU!!!!: Przepraszam za pomylke... odp D napisalem z innego zadania
prawidlowe odp wygladaja tak:
A {1;2;3;4;5;6;}
B R − {4}
C <−2;∞)
D (2;∞)
jeszcze raz przepraszam....
ale inna metoda dobrnolem do takiego etapu
x≥
−2x−2√2
pomoze ktos dalej?
19 gru 16:42
123_123_123_123: Nie ma opcji...
x∊R
Zresztą co ty tworzysz jakieś sposoby?
Tutaj trzeba rozwiązać proste równanie kwadratowe
19 gru 16:44
Licealista: | | 2x | |
mianownik nie może być równy zero  np. funkcja f(x)= |
|
|
| | (x−2)2 | |
D=R\{2} dlatego że przez 0 nie możesz dzielić, nie musisz twgo aż tak przekształcać jak to
zrobiłaś wyżej
19 gru 16:49
123_123_123_123: Licealista przeczytałeś chociaż pierwszą wiadomość?
Gdzie ty w tym f(x)=√x2 − 2√2x + 2 masz mianownik?
19 gru 16:51
Licealista: podpowiem Ci że że musisz wykorzystać kwadrat sumy z x i √2
19 gru 16:51
Licealista: to przykład, nie chcę dawać gotowca, tu zrobię a na sprawdzianie jej nie pomogę, to był
przykład
19 gru 16:52
Licealista: sorry kwadrat różnicy tam ma być... sorka.
19 gru 16:53
123_123_123_123: To teraz wytłumacz co twój przykład ma wspólnego z zadaniem gdzie jest pierwiastek?
Przy pierwiastkach wyrażenie podpierwiastkowe musi być ≥ 0, co już napisałem dawno.
Zreszta zadanie tez już dawno rozwiązane
19 gru 16:53
Licealista: to tak, żeby wyznaczyć dziedzinę trzeba znaleźć takie liczby które nie dadzą liczby ujemnej pod
pierwiastkiem ponieważ działanie typu,
√−x nie ma sensu w matematyce, tak samo jak
dzielenie przez zero. Caman
19 gru 16:56
Aga1.: √−x istnieje w R gdy −x≥0, czyli x≤0
19 gru 16:59
Licealista: moim skromnym zdaniem 19gru o 16:22 zostało obliczone miejsce zerowe, ale wiecie lepiej ok.
19 gru 17:01
123_123_123_123: Nie idioto została obliczona nierówność x2 − 2√2x + 2 ≥ 0 która jednocześnie jest dziedziną
wyrażenia f(x)=√x2 − 2√2x + 2
19 gru 17:05
krystek: @123.. a Tobie byłoby przyjemnie gdyby Ciebie tak nazwano?
19 gru 17:07
Równy: Z twoja mamą
19 gru 17:14
olaa: pomozcie mam do rozwiazania : dla argumentu 2√2 funkcja f(x)=24 − x3/√2 przyjmuje wartosci
A;8 B 4√2 C −4√2 D−8 √2
19 gru 17:32
Dominik: podstaw 2√2 za x, wynik jest twoim rozwiazaniem.
19 gru 17:33
olaa: a za ten z przy x3 też?
19 gru 17:42
xxxx: zbiorem wartosci funkcjii f(x) =−x−3 gdzie x nalezy do<−2;3)
19 gru 17:49
xxxx: oblioczy ktoś?
19 gru 17:49