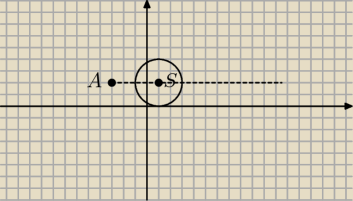
Proszę o pomoc - > Geometria analityczna Uczeń : W trójkąt równoboczny ABC, którego wierzchołek A=(−3,2), wpisano okrąg o środku S=(1,2). Oblicz współrzędne punktów styczności tego okręgu z bokami trójkąta ABC.

think:

	1
Okrąg wpisany w trójkąt równoboczny ma r =		h
	3

	2
odcinek AS to		h można nawet z rysunku odczytać, że w takim razie r = 2
	3

h = 6 pierwszy punkt styczności ma współrzędne (3, 2) wierzchołki tego trójkąta mają współrzędne B = (3, 2 + 2√3) oraz C = (3, 2 − 2√3) a współrzędne punktów styczności to średnie arytmetyczne odcinków wyznaczonych przez kolejne wierzchołki. czyli musisz wyznaczyć środek odcinka AB i AC ponieważ BC już masz.

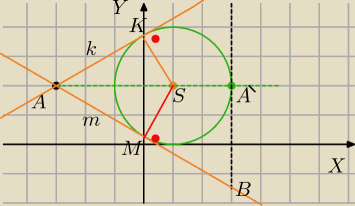
Mila: A=(−3,2), S=(1,2), |AS|=4 r=2 A' punkt styczności, A' =(3,2) odległość prostej AC od punktu S jest równa r=2 Bok AC tworzy kąt 30⁰ z prostą AS Bok AB tworzy kąt 30⁰ z prostą AS i AS II OX Prosta AC: k: y=ax+b

	√3		√3
k : y=		x+b i A∊k⇔2=		*(−3)+b⇔b=√3+2
	3		3

	√3
k: Y=		x+√3+2
	3

	√3		√3
prosta AB:y=−		x+b i 2=−		*(−3)+b⇔b=−√3+2
	3		3

	√3
m: y=−		x−√3+2
	3

	3
SM⊥m ⇔ y=		x+b i S∊prostopadłej⇔ 2=√3*1+b⇔b=2−√3
	√3

SM: y=√3x+2−√3

	√3
Układ: y=√3x+2−√3 i y=−		x−√3+2
	3

x=0 i y=2−√3 ⇔M=(0;2−√3) Drugi punkt (K) jest symetryczny do M względem AS x=0 y=2+√3 ( z równania prostej k) K=(0;2+√3)