zadanie tn: Z klasy, w której jest 20 dziewcząt i 5 chłopców wybieramy 3 osobową delegację. Jakie jest prawdopodobieństwo, że w skład delegacji wejdzie co najmniej jeden chłopiec? Omegą są wszystkie delegacje, zdarzeniem A, są wszystkie możliwe wyniki, czyli chłopak, chłopak, chłopak lub dziewczyna, dziewczyna, chłopak lub, chłopak, chłopak, dziewczyna. Rozwiązać potrafię, ale jak ładnie zapisać omegę i zdarzenie A?

Dominik:

	25 3
|Ω| =

|A| = 20 * 19 * 5 + 20 * 5 * 4 dopiero zaczalem prawdopodobienstwo. czy to jest prawidlowe?

Eta: Zb. Ω −− jest zbiorem wszystkich zdarzeń elementarnych, które są trójelementową kombinacją ze zbioru 25− elementowego

tn: A omów co zrobiłeś? Masz zamiar "wyszczęścić" delegacje z jednym chłopakiem, dwoma, lub trzema. Jaką masz szansę, że wyszczęścisz z zamkniętymi oczami taką właśnie delegację spośród ... możliwych.

Dominik: |A| = 20 * 19 * 5 + 20 * 5 * 4 + 5 * 4 * 3 o w ten sposob, tak mi sie wydaje. pierwszy iloczyn reprezentuje uklad dziewczyna dziewczyna chlopak, drugi dziewczyna chlopak chlopak, trzeci chlopak chlopak chlopak. dobrze?

tn: rzucamy dwiema kostkami. Jaka jest szansa, że uzyskamy sumę oczek podzielną przez 4 WIęc |Ω| = 36 A = { (3,5); (5,3); (2,6); (6,2); (4,4) } Dobrze to ?

Mila:

	25 3
|Ω|=		na tyle sposobów mozna wybrać 3 osoby z 25.

A− wybrano jednego chłopca i 2 dziewczynki lub wybrano 2 chłopców i 1 dziewczynkę lub wybrano 3 chłopców

	5 1		20 2		5 2		20 1		5 3		20 0
|A|=		*		+		*		+		*		oblicz

	|A|
P(A)=
	|Ω|

II sposób A' − wybrano 3 dziewczynki

	20 3
|A' |=

	|A' |
P(A)=1−
	|Ω|

Dominik: a (1, 3), (3, 1), (6, 6) (6, 6) i drugie (4, 4)?

tn: Rozważ chłopak chłopak chłopak: Twoje rozumowanie zwraca każdy ciąg. Dla ciebie kolejnośc nie gra roli. Powinieneś wybierać podzbiory, a nie ciągi. Nie ma tutaj nic do rzeczy, kogo wybierasz, ale na ile sposobów wybierasz.

tn: Faktycznie Mila, odwrotnym zdarzeniem jest to, że nie wzięto chłopaka

tn: @Mila, pomożesz z kombinatoryką?

Mila: 2) |Ω|=6² A − suma oczek podzielna przez 4 Mozliwe sumy podzielne przez 4: 4;8;12 A={(1,3); (3,1); ( 3,5); (5,3),(4,4); (2,6),(6,2),(6,6)} W takim zadaniu radzę wypisać wszystkie zdarzenia elementarne, prawie zawsze podobne zadanie jest na maturze, a łatwo coś zgubić i punkty stracic.

tn: Ok.A jeśli iloczyn oczek ma być mniejszy niż 11 ?

Mila: [Ntn]]− zdarzenie przeciwne. ( nie odwrotne)

tn: ok

Mila: B− iloczyn oczek mniejszy od 11. Popatrz na wszystkie zdarzenia elementarne i wypisz elementy zbioru B. Sprawdzę.

tn: (1, 1) (1, 2) (1, 3) (2, 1) (2, 2) (2, 3) (3, 1) (3, 2) (3, 3) (4, 1) (4, 2) (5, 1) (5, 2) (6, 1) (7, 1) (8, 1) (9, 1) (10, 1)

tn: powinno być tych par 19.

Eta:

Eta: @tn .......... na kostce nie ma oczek 7,8,9,10

tn: Ok, ale napisałem bzdury −wstyd mi A Mam zadanie: Student zna odpowiedzi na 30/45 pytań. Jeśli dobrze odpowie na 4 pytanie ma 5, jeśli 3 to 4, jeśli dwa to trójkę. Losuje 4 pytania. a) Jaka jest szansa żeby dostał 5 ? b) Jaka jest szansa, że będzie to ocena ≥3

tn: (generowałem te numerki, i nie przemyślałem co kopiuję )

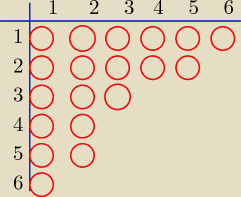
Mila: Co za głupstwa wypisałeś? Rzucamy dwiema kostkami sześciennymi. Jakie jest prawdopodobieństwo że iloczyn oczek na obu kostkach jest mniejszy od 11. [Iloczyn to wynik z mnożenia. ] B={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5), (3,1),(3,2),(3,3), (4,1),(4,2), (5,1),(5,2), (6,1)} |B|=19

	19
P(B)=
	36

Mila: Tn, rób samodzielnie zadanie ze studentem, podobne do pierwszego.