zabadaj przebieg zmienności funkcji f ladypi: Hej mam taki przykład do zrobienia na ćwiczenia, nie bylo mnie na wykladzie i nie bardzo to ogarniam, bylabym wdzieczna gdyby ktos napisal mi tak w punktach po kolei jak to zrobic Zbadaj przebieg zmienności funkcji f i narysuj jej wykres: f(x)= x⁴− 5x² +4

Vizer: 1. Dziedzina 2. Asymptoty 3. Punkty charakterystyczne 4. Parzystość/Nieparzystość 5. Ekstrema lokalne 6. Monotoniczność 7. Punkty przegięcia 8. Wypukłość/ wklęsłość 9. Piękny rysunek na podstawie punktów 1−8

ladypi: to juz cos, a czy ktos mogłby to rozwiazac? bo potrzebny mi jest juz konkretny przyklad na liczbach...

Krzysiek: przykład: http://www.matematyka.pl/281113.htm

Mila: http://www.math.com.pl/analiza-matematyczna-1/badanie-przebiegu-zmiennosci-funkcji/ Tu masz przykłady z wyjasnieniem.

ladypi: dziedziną jest zbiór licz rzeczywistych?

Mila: Dla Twojej funkcji tak, bo występujące tam potegowaniei i dodawanie jest wykonalne.

Mila: To Ci pomoże? Rób według procedury podanej przez Wizera Sprawdzę Ci po 21.

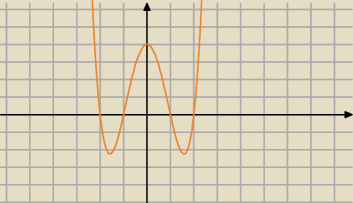
ladypi: Dobra nie jestem pewna ale chociaz troche^^ Dziedzina funkcji x∊R granica na końcach przedziałów +∞ funkcja parzysta punkty przeciecia z osią Ox będą 4? jeden w przyblizeniu 3,2 nie podaje reszty bo nie wiem czy to dobrze rozkminilam... Oy 4 I pochodna 4x³−10x 4x³−10x=0 2x (2x²−5) x=0 2x²−5=0 2x²=5 /2 x²=2,5 x= √2,5 ? II pochodna 12x²−10 2 (6x²−5) hmmm... co za mordownia...−.−

ladypi: pomoże ktoś?:(

Mila: 1) D=R 2) miejsca zerowe: x⁴−5x²+4=0 x²=t; t≥0 t²−5t+4=0 Δ=25−16=9

	5−3		5+3
t1=		=1 lub t2=		=4
	2		2

x²=1 lub x²=4 x+1 lub x=−1 lub x=2 lub x=−2 3) Monotoniczność: obliczam f '(x)=4x³−10x Miejsca zerowe pochodnej:( ewentualne ekstrema)

	5
4x3−10x=0⇔x(4x2−10)=0 ⇔x=0 lub x2=		⇔
	2

	√10		√10
x=0 lub x1=		lub x2=−
	2		2

	√10		√10		√10		√10
f '(x)>0⇔x(x−		)(x+		)>0⇔x∊(−		;0)∪ (		;∞)
	2		2		2		2

w tych przedziałach funkcja jest rosnąca

	√10		√10
f'(x)<0 dla x ∊(−∞;−		)∪(0;		) w tych przedziałach funkcja jest malejąca
	2		2

	√10		9
dla x=−		osiąga minimum lokalne : ymin=−
	2		4

dla x=0 osiąga maksimum lokalne; y_maks=4

	√10		9
dla x=		osiąga minimum lokalne :ymin=
	2		4

4) f ''(x)=12x²−10 miejsca zerowe: x=√5/6 lub x=√5/6 zbadaj czy zmienia się znak w tych punktach, to będą punkty przegięcia 5) granice

	5		4
limx→−∞(x4−5x2+4)=limx→−∞(x4(1−		+		))=∞
	x2		x4

	5		4
limx→∞(x4−5x2+4)=limx→∞(x4(1−		+		))=∞
	x2		x4

ladypi: dzieki, teraz ogarne

Mila: powodzenia.