Stereoetria
Kin: Podstawą prostopadłościanu jest prostokąt , którego jeden z boków jest od drugiego o 2 dłuższy.
przekątna tego prostokąta tworzy z jego dłuższym bokiem kąt o mierze 30 stopni. przekątna
prostopadlościanu tworzy z płaszczyzną jego podstawy kąt o mierze 60 stopni. wyznacz objętość
prostopadłościanu.
Siedzę nad ty już godzinę i za każdym razem wychodzi inny wynik. Będzie ktoś pomocny?
17 gru 22:54
Kin:
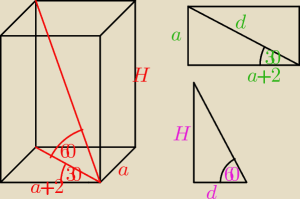
Wychodzi mi że:
d=2a
H=2
√3a
V wychodzi jakieś dziwne. Dobrze to rozumuje?
17 gru 23:22
wartość przybliona:
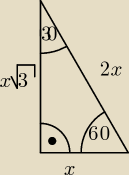
takie coś znasz? wystarczy podstawić dwa razy: najpierw do trójkąta w podstawie, a później do
tego, którego przeciwprostokątną jest przekątna prostopadłościanu
17 gru 23:37
Mila:
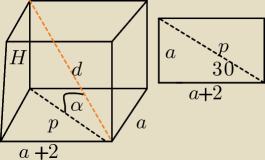
α=60
√3*(a+2)=3a⇔
√3a+2
√3=3a⇔
3a−
√3a=2
√3
a(3−
√3)=2
√3
| | a | | 1 | | a | | 4√3 | |
sin30= |
| ⇔ |
| = |
| ⇔p=2a= |
| |
| | p | | 2 | | p | | 3−√3 | |
| | 4√3 | | 12 | | 12 | | 3+√3 | |
H=p*√3= |
| *√3= |
| = |
| * |
| = |
| | 3−√3 | | 3−√3 | | 3−√3 | | 3+√3 | |
| | 2√3 | | 3+√3 | | 2*3√3+2*3 | | 6√3+6 | |
a= |
| * |
| = |
| = |
| =√3+1 |
| | 3−√3 | | 3+√3 | | 9−3 | | 6 | |
a+2=
√3+1+2=
√3+3
V=(
√3+1)*(
√3+3)*2(3+
√3)=(2
√3+2)(9+6
√3+3)=
=(2
√3+2)(12+6
√3)=24
√3+24+36+12
√3=60+36
√3
17 gru 23:45
 Wychodzi mi że:
d=2a
H=2√3a
V wychodzi jakieś dziwne. Dobrze to rozumuje?
Wychodzi mi że:
d=2a
H=2√3a
V wychodzi jakieś dziwne. Dobrze to rozumuje?
 takie coś znasz? wystarczy podstawić dwa razy: najpierw do trójkąta w podstawie, a później do
tego, którego przeciwprostokątną jest przekątna prostopadłościanu
takie coś znasz? wystarczy podstawić dwa razy: najpierw do trójkąta w podstawie, a później do
tego, którego przeciwprostokątną jest przekątna prostopadłościanu
 α=60
α=60