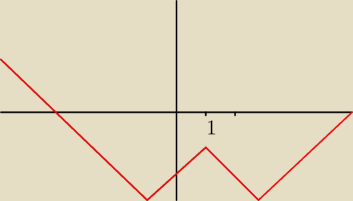
"Łatwe" Zadania na Poniedziałek- częśc druga Next: WYKRES DO ZADANIA 12! Miałem to wrzucić jutro ale znalazłem chwilkę czasu wolnego i wrzucam Druga część mej nieszczęśliwej pracy na poniedziałek Zasady jak przedtem sprawdźcie i poprawcie jak możecie xD

	−1		k−3		1
Zad1. Wyznacz k wiedząc, że dla x=		wyrażenie		−4x przyjmuje wartość
	2		2		2

MOJE ROZWIĄZANIE: Dla k=0

	1		1−√3
Zad2. Doprowadź do najprostszej postaci wyrażenie liczbowe		+
	√3−1		2

MOJE ROZWIĄZANIE: Mi wyszło że to się =0 nie wiem czy o to chodziło Zad3.Dane są zbiory A= {x ∊R : √x²−10x+25≤3} B= {x ∊R : |x+1|>4} Wyznacz sumę zbiorów A i B MOJE ROZWIĄZANIE: A U B=(3,8) Zad4.Dany jest punkt A=(−1,1), oraz wektor AB=[2,3]. Wyznacz współrzędne punktu B oraz współrzędne środka odcinka AB.

	5
MOJE ROZWIĄZANIE: B=(1,4), Środek AB=(0,		)
	2

Zad5.Podaj równanie prostej prostopadłej do prostej 2x−y+1=0 przechodzącej przez punkt M=(1,−2)

	1		3
MOJE ROZWIĄZANIE: y=−		x −
	2		2

Zad6.Dla jakich wartości parametrów A i B układ równań Ax+3y=5 2x+y=B jest sprzeczny? NIE MAM ROZWIĄZANIA : PROSZĘ O POMOC Zad7.Wykonaj odpowiednie przekształcenia wykresu funkcji y= |x|, aby uzyskać wykres funkcji f(x)=1−|x−2| MOJE ROZWIĄZANIE: Nie narysuję tu bo nie wiem jak ale opisze: 1.Rysuję wykres funkcji f(x)=−|x| (z ramionami skierowanymi w dół) 2.Przesuwam go o 2 w → i otrzymuję wykres f(x)=−|x−2| 3.Przesuwam go o jeden w górę i otrzymuję wykres f(x)=1−|x−2| TAK? Zad8. Oblicz pole trójkąta określonego układem nierówności y≤2−|x| y≥−1 MOJE ROZWIĄZANIE: Też nie mam jak narysować więc dam tylko wynik: Pole=9 Zad9.Zbadaj wzajemne położenie okręgów o równaniach (x−1)²+(y−2)²=4 x²+y²−8x−12y+43=0 MOJE ROZWIĄZANIE: Rysuję i zauważam że okręgi są styczne zewnętrznie Zad10.Określ dziedzinę oraz miejsce zerowe funkcji

	x2−4
f(x)=
	1−|x|

MOJE ROZWIĄZANIE: Tego to za bardzo nie wiem ale wyszło mi że Df=R\{1,−1} A miejsca zerowe to x=2 i x=−2 Zad11. Rozwiąż równanie 2|x−3|=x MOJE ROZWIĄZANIE: W przedziale (−∞,3) dla x=2 a w przedziale (3,+∞) dla x=6 Zad12.Dany jest wykres funkcji. (TEN NA SAMEJ GÓRZE) Określ przedziały monotoniczności funkcji oraz oś symetrii jej wykresu. MOJE ROZWIĄZANIE: Dla x należącego: (−∞,−1> maleje (−1,1>rośnie (1,3>maleje (3,+∞)rośnie Środek symetrii odczytuję z wykresu i jest to x=1 Zad13.Jak zmieni się pole prostokąta, jeśli jego długość zmniejszymy o 20% a szerokość zwiększymy o 25%?

	80		125		10000
MOJE ROZWIĄZANIE: Nie zmieni się, gdyż P=		a*		b=		ab=ab
	100		100		10000

Zad14.Oblicz miarę kąta wewnętrznego dwudziestokąta foremnego. NIE MAM ROZWIĄZANIA : PROSZĘ O POMOC Zad15.Wyznacz dwie liczby, których suma wynosi 30, a różnica ich kwadratów 120. MOJE ROZWIĄZANIE: Są to liczby x=17 i y =13 Ufff KONIEC

tim: Mój post. Zaklepuję.

Next: Wybawiciel

tim: 1. OK. 2. Nie można zrobić tak, jak zapewne zrobiłeś: PRZEWIDYWANE TWOJE ZŁE ROZWIĄZANIE:

1		1 − √3		1(√3 − 1)		1 − √3
	+		=		+		= 0
√3 − 1		2		2		2

POPRAWNE ROZWIĄZANIE:

1		1 − √3
	+		= ... do wspólnego mianownika!
√3 − 1		2

2		1		√3 − 1		1 − √3
	*		+		*		= ...
2		√3 − 1		√3 − 1		2

2		(1 − √3)(√3 − 1)
	+		= ...
2(√3 − 1)		2(√3 − 1)

2 + √3 − 1 − 3 + √3
	= ...
2(√3 − 1)

2√3 − 2
	= 1
2√3 − 2

Next: Ahh no tak dzięki, jeszcze nie jestem do końca wtajemniczony w tajniki matematyki

tim: 3. Prawie dobrze. Sprawdź jeszcze raz 4. −−−−−−−−−−−−−−−−−− 5. DOBRZE. 6. Miałeś metodę wyznaczników?

Next: No pewnie że miałem

tim: 7. −−−−−−−−−−−−− 8. DOBRZE 9. −−−−−−−−−−−−− 10. DOBRZE 11. A dla 3? 12. Jeżeli w poleceniu masz przedziały to WSZYSTKIE ( ), jeżeli MAKSYMALNE to zawsze < >, chyba, że wyklucza je dziedzina. 13. DOBRZE

	360		(n − 2) * 180
14. Wzór: 180 −		lub		na kąt w n−kącie foremnym.
	n		n

15. DOBRZE

Next: Wiem, w 3 ma być (−∞,−5)U<2,+∞)

tim: To rozwiąż mi tutaj zadanie 6, metodą wyznaczników. Układ jest sprzeczny jeśli W=0 i W_x ≠ 0, lub W=0 i W_y ≠ 0.

Next: W 11 dla 3 nie może być bo by wyszło że 0=3 co jest sprzeczne

Next: Wiesz co zapomniało mi się tego trochę, jutro się nad tym pomęczę, najpierw przeanalizujmy te łatwiejsze

tim: Na pewno trzecie ma byc: "(−∞,−5)U<2,+∞) "

tim: 11. OK. 6. Ok, jak rozwiążesz, napisz

Next: Możesz mi jeszcze powiedzieć co z 3, 7 i 9?

tim: A pokaż mi jak rozwiązałeś 9. 3 napisałem ci pytanie wyżej. 7 − nie pomogę, przykro mi

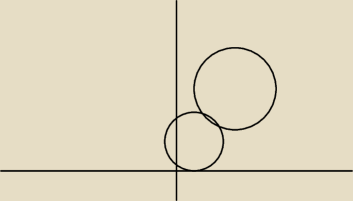
Next: Pół kratki to 1, nie wiem czy mi to żle wyszło czy one się rzeczywiście przecinają

Next: Jeszcze do 9 (x−1)²+(y−2)²=4 z wzoru (x−a)²+(y−b)²=r² odczytuję że środek S(a,b) = S(1,2) a r=2 x²+y²−8x−12y+43=0 ze wzoru x²+y²−2ax−2by+c=0 odczytuję że a=4, b=6 czyli S=(4,6) a r obliczam ze wzoru r=√a²+b²−c=3

Next: Powiedzcie mi jeszcze proszę czy w 3 zad. rozwiązaniem jest przedział (−∞,−5) U <2,+∞) ? Ważne jest to dla mnie