Kąty koła i okręgi karmazynowy msciciel: W równoległoboku narysowano dwa półokręgi: średnicą jednego okręgu jest krótszy bok, a drugiego − dłuży bok równoległoboku. Półokręgi przecięły się wewnątrz równoległoboku w punkcie P. Wykaż, że punkt P należy do przekątnej równoległoboku. No niby na rysunku wszystko smiga ale jak to udowodnic

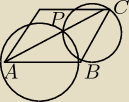
Sever: Wystarczy pokazać, że punkty A P i C są współliniowe: Kąt APB oparty jest na średnicy więc jego miara wynosi 90 Kąt BPC oparty jest na średnicy więc jego miara wynosi 90 Z powyższego mamy, że: Kąt APC wynosi 180 stopni