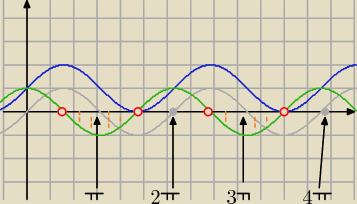
Trygonometria Maciek: Może ktoś mi pomóc z pewnym zadankiem Narysuj w jednym układzie współrzędnych wykresy funkcji f(x)=cosx i g(x)=sinx+1 dla x∊<0;4π>. Na podstawie wykresu podaj a) miejsca zerowe funkcji g(x) b) przedziały, w których obie funkcje są jednocześnie malejące c) rozwiązanie nierówności cosx(sinx+1)<0

	3		7
a) x0 ∊{		π ;		π}
	2		2

	1		5
b) x∊(		π ; π) ∪ (		π; 3π)
	2		2

ale właśnie z podpunktem c) mam problem, nie wiem jak to rozwiązać..:(

Maciek: pomoże ktoś

Maciek: nikt mi nie pomoże

Maciek: może mi ktoś pomóc

Mat: y=cosx to jest w tablicach przecież ...

Mila: cosx(sinx+1)<0⇔ cosx<0 i sinx+1>0

	π		3π		5π		7π
x∊(		:		)∪(		;		)
	2		2		2		2