Monotoniczność.
Patri: | | ⎧ | x gdy x<0 | |
| f(x)= | ⎨ | |
|
| | ⎩ | x+1 gdy x≥0 | |
Funkcja jest rosnąca.
Jak poprawnie zapisać odpowiedź na pytanie o monotoniczności?
Rośnie w całej dziedzinie czy jest rosnąca przedziałami?
17 gru 17:29
Patri: Prooooosteeee, podbijam.
17 gru 17:49
Patri: podbijam
17 gru 18:08
Patri: Rośnie w całej dziedzinie czy jest rosnąca przedziałami?
17 gru 18:23
Patri: ?
17 gru 18:34
Patri: up
17 gru 18:45
Patri: up
17 gru 19:12
Patri:
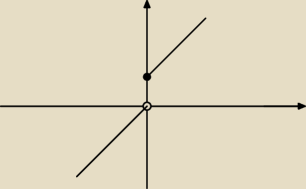
Jak poprawnie zapisać odpowiedź na pytanie o monotoniczności?
Rośnie w całej dziedzinie czy jest rosnąca przedziałami?
17 gru 19:13
Patri: 
17 gru 19:31
Patri:
17 gru 19:59
Dominik: spojrz na wykres i odpowiedz na pytanie.
17 gru 20:01
Dominik: inaczej: widzisz gdzies przedzial w ktorym maleje?
17 gru 20:02
Patri: nigdzie, ale również nie widzę nigdzie w takiej sytuacji:
| | ⎧ | x gdy x<0 | |
| y= | ⎨ | |
|
| | ⎩ | x−1 gdy x≥0 | |
a tu definicja "rośnięcia" nie jest spełniona.
I dzięki żeś się nade mna zlitował. Myślałam, ze zostanę z rozważaniami sama...
17 gru 20:06
Patri:
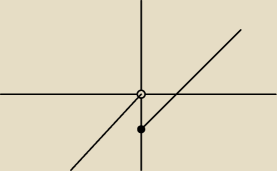
widzisz?
17 gru 20:07
Patri: no i zostałam sama...
17 gru 20:16
Dominik: przyjrzyj sie wykresowi. dla x=0 funkcja zmalala.
17 gru 20:38
Patri: O ten wykres wyżej mi chodzi i o sformułowanie odpowiedzi do zadania.
Rosnąca w całej dziedzinie czy rosnąca przedziałami, która z tych odpowiedzi będzie poprawna?
18 gru 09:09
krystek: Rosnąca w całej dziedzinie , Nie ma oddzielnych przedziałów , określona jest dla x∊R
18 gru 09:21
Artur_z_miasta_Neptuna:
nie jest rosnąca w całej dziedzinie
ponieważ istnieją dwa takie 'x
1,x
2', że x
1<x
2 a zachodzi f(x
1)>f(x
2)
ale jest rosnąca przedziałami
18 gru 09:22
krystek: f↗dla x∊(−∞,0) i dla x∊<0,∞) i koniec
18 gru 09:24
Patri: Artur, ok, co do tego dolnego wykresu to się zgadzam, mi chodzi o ten na samym początku.
Niby jest rosnąca w całej dziedzinie, spełnia definicję, którą wpisałeś, ale jest nieciągła,
dlatego mam taki dramat w głowie.
18 gru 09:25
Patri: Dzięki Krystek.
18 gru 09:25
Aga1.: Jeśli masz dylemat, to zapisz , funkcja jest rosnąca w każdym z przedziałów (przedziałów nie
łącz sumą ) i będzie dobrze.
Ta funkcja nie jest rosnąca dla x∊R, co zostało już napisane.
18 gru 09:34
Artur_z_miasta_Neptuna:
krystek ... przedziały otwarte są przy monotoniczności
nie ma czegoś takiego, że funkcja jest rosnąca w punkcie 0
18 gru 09:39
Aga1.: A jeśli w zadaniu jest polecenie, "podaj maksymalne przedziały monotoniczności"?
Myślę,że krystek podała poprawną odpowiedź.
Można podać nieco inną odpowiedź ( przedziały otwarte)
18 gru 09:58
krystek: I tutaj Artur możemy podyskutować ,
w def którą podałeś x−1−x2 muszą należec do dziedziny.
Ale funkcja roście od x=0 do ∞, nie napisałam ,że jest rosnąca w punkcie.
Dyskusyjne jest wtedy gdy nie mamy napisane max przedziały ,ale to nie jest błędem .
18 gru 10:11
Artur_z_miasta_Neptuna:
krystek ... to jak wykażesz, że funkcja na przedziale <0;+
∞) jest rosnąca
co do przedziału
(0,+
∞) nikt wątpliwości nie ma ... a więc prosze o udowodnienie, ze jest rosnąca w punkcie 0
18 gru 10:33
Artur_z_miasta_Neptuna:
krystek ... monotoniczność tak samo jak różniczkowalność zapisuje się przedziałami otwartymi.
powiedz mi ... czy funkcja f(x)=x2 ... rośnie w przedziale <0;+∞) czy (0,+∞) ?
18 gru 10:35
krystek: Ale jesteśmy na etapie szkoły sredniej i tutaj były dyskusje i zaczęto dodawać max przedziały.
Tak jak piszemy ,że x2+1 =0 nie ma pierwiatków i nie dodajemy w liczbach R.
18 gru 10:38