zadania na sprawdzian geometria analityczna PILNE hubert71: Witam Mam do zrobienia zadania na jutro, od których mozna powiedziec zalezy to, czy zdam. oto pierwsze: 1. Wyznacz równianie okręgu o środku S(−1,2) i promieniu 4. Narysuj ten okrąg. Oblicz jego punkty przecięcia z osiami układy współrzędnych. 2. Oblicz odległośc między prostymi y= 2x + 1 y=2x − 4 3. Punkty A(1,2) , B(13,4), C(7,10). Oblicz pole trójkąta ABC. 4. Dane są zbiory punktów określone nierównościami: A: x² −6x + y² + 12y ≤ 4 i B: 3x + y −3 ≥ 0. Narysuj figurę F= A ∩ B i wyznacz jego pole. 5. Wyznacz miary kątów ograniczonych prostymi: y= √3/3x − 2, y= √3x + 3, x6 w zadaniu piątym, pierwsza prosta to jest pierwiastek z 3 w liczniku, a 3 z kolei jest w mianowniku. Czyli pierwiastek z 3 dzielony na 3 i to jest ta liczba x

Tad: ... jeśli z takimi masz problem ... −:(

hubert71: jak ty nie masz problemu, to pomoz

hubert71: chociaz jedno ? :C 1 zrobiłem ledwo co, ale reszta to czarna magia

slawek: Zad. 2 linia różowa y=2x−4 linia pomarańczowa y=2x+1 linia niebieska = 1 linia zielona = 2 linia czerwona =x pitagorasem 2² + 1² = x² 4 + 1 = x² √5 = x <<<< To twoja odpowiedz

slawek: mozesz to sobie oczywiscie policzyc ze wzoru na odleglosc punktu od prostej ale zajmie ci to wiecej czasu

slawek: Zad.4 Przekształć podany wzór na równanie okręgu, odczytaj promień i środek okręgu. Nanieś wszystko na układ współ. Narysuj prostą y≤−3x+3 i zaznacz cześć wspólną, która znajduje się pod prostą na okręgu...

hubert71: sławek, mi to nic nie mowi

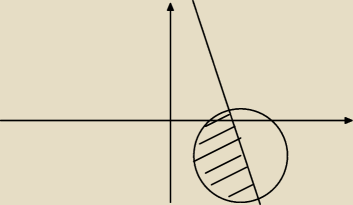
slawek: Powinno to wyglądać mniej więcej tak, wzór przekształcamy aby uzyskać wartość promienia oraz środek okręgu na układnie wsp. Wzóry wygląda następująco: (x−3)²+(y+6)² ≤ 49 To znaczy, że promień okręgu wynosi r=7, a środek okręgu wynosi S(3;−6) Wystarczy go narysować na układnie dodać prostą i oznaczyć. Znak ≤ Czyli mniejszości lub równości oznacza, że powinniśmy zaznaczyć część wewnątrz koła oraz znak ≤ przy równaniu prostej mówi nam, że powinniśmy zaznaczyć obszar poniżej funkcji ( znak mniejszości lub równości zaznaczamy linią ciągłą, gdy mamy do czynienia ze znakiem < lub > rysujemy linię przerywaną)