 Witam, proszę o pomoc z zadaniem:
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają długość a. W ostrosłup ten
wpisano sześcian tak, że cztery jego wierzchołki należą do podstawy ostrosłupa, a pozostałe
cztery leżą na jego krawędziach bocznych. Oblicz długość krawędzi sześcianu.
Moje obliczenia(w skrócie):
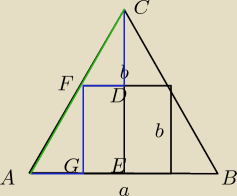
IACI=√32a=ICBI (wysokość ściany bocznej−trójkąta równobocznego)
ICEI=√22a
IDCI2+IFDI2+IGFI2+IAGI2=IACI2
(√22a−b)2+(b2)2 +(a2−b2)2 +b2= (√32a)2
2,5b2−ab(√2+12)=0
b=25(√2+12)a
Podczas gdy w odpowiedziach jest wynik a(√2−1)
Witam, proszę o pomoc z zadaniem:
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają długość a. W ostrosłup ten
wpisano sześcian tak, że cztery jego wierzchołki należą do podstawy ostrosłupa, a pozostałe
cztery leżą na jego krawędziach bocznych. Oblicz długość krawędzi sześcianu.
Moje obliczenia(w skrócie):
IACI=√32a=ICBI (wysokość ściany bocznej−trójkąta równobocznego)
ICEI=√22a
IDCI2+IFDI2+IGFI2+IAGI2=IACI2
(√22a−b)2+(b2)2 +(a2−b2)2 +b2= (√32a)2
2,5b2−ab(√2+12)=0
b=25(√2+12)a
Podczas gdy w odpowiedziach jest wynik a(√2−1)
| b/2 | a/2 | |||
ale prościej | = | |||
| CE−b | CE |
| a*CE | ||
b= | =...=a(√2−1) | |
| CE+a |
