Zadanie z lasem maniek: Sosnowy las, składający się z 4500 drzew, rośnie na obszarze w kształcie kwadratu o boku długości 1 km. Każde z drzew ma średnicę nie większą niż 0,5 m. Wykazać, że w pewnym prostokącie 10m x 20m nie rośnie żadne drzewo. Jak to udowonic

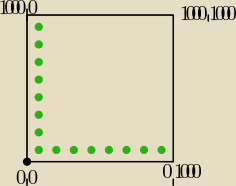
Artur_z_miasta_Neptuna: krok 1. ustawiamy postokąt 20x10 w lewym dolnym rogu krok 2 . umieszczmy drzewo w najbardziej odpowiednim dla nas miejscu czyli w po środku górnej belki prostokąta i zakładamy, ze jego średnica to 0.5m. krok 3. poruszamy prostokątem 'w górę', aż drzewo ... zniknie z ramki prostokąta. lewy dolny róg prostokąta jest o 10.5m wyżej niż był wcześniej ... stawiamy kolejne drzewo ... itd. itd. krok 4 takich drzew ustawiliśmy 96 krok 5 teraz ustawmy na moment prostokąt w pozycji 10x20 także w lewym dolnym rogu i poruszamy go w 'poziomie' następne drzewo (pierwsze jest umieszczone 10.25 od granicy działki) będzie umieszczone dokładnie 10.5 dalej ile w takim razie powstanie 'rzędów' w poziomie tyle samo w pionie ... czyli 96 krok 6 stąd ... drzew tych musi być 96*96 = 9'216 uwaga ... zadanie jest rozwiązane przy założeniu, ze prostokąt można obrócić pod dowolnym kątem a nie jest sztywno 10m w poziomie i 20m w pionie

Artur_z_miasta_Neptuna: wersja z tym zastrzeżeniem jest analogicznia tylko w pionie nie sadzimy co 10.5m tylko co 20.5m

Artur_z_miasta_Neptuna: reasumując: aby w dowolnie obranym prostokącie o wymiarach 10x20 znajdował się chociażby skrawek drzewa o średnicy dokładnie 0.5m potrzeba: a) 96*96 = 9'216 b) 49*96 = 4'704 drzew o takiej średnicy. A przecież w lesie rośnie tylko 4'500 drzew ... i żadne z nich nie ma chociażby 0.5m średnicy.