| 1 | 1 | ||
e= | f+7=a | ||
| 2 | 2 |
| 1 | |
f=b | |
| 2 |
| 1 | 1 | |||
( | f+7)2=169− | f2 | ||
| 2 | 4 |
| 1 | 1 | ||
f2+7f+49+ | f2−169=0 | ||
| 4 | 4 |
| 1 | |
f2+7f−120=0 | |
| 2 |
| −b+√∆ | −7+17 | |||
f>0 f= | = | =10 | ||
| 2a | 2*1/2 |
| e*f | 24*10 | |||
P= | = | =120 | ||
| 2 | 2 |
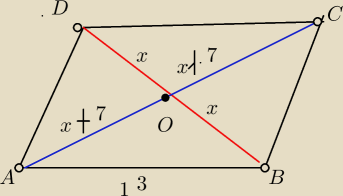 |AB|=|BC|=|CD|=|AD|=13
|BO|=OD|=x>0
|DB|=2x
|AO|=OC||=x+7>0
|AC|=2x+14
|AB|2=|AO|2+|OB|2
132=(x+7)2+x2
169=x2+14x+49+x2
2x2+14x+49=169
2x2+14x−120=0
x2+7x−60=0
x=−12 cm (nie należy dziedziny
lub x=5cm (należy do dziedziny
|BD}=2x=2*5=10cm
|AC|=2x+14=2*5+14=24cm
|AB|=|BC|=|CD|=|AD|=13
|BO|=OD|=x>0
|DB|=2x
|AO|=OC||=x+7>0
|AC|=2x+14
|AB|2=|AO|2+|OB|2
132=(x+7)2+x2
169=x2+14x+49+x2
2x2+14x+49=169
2x2+14x−120=0
x2+7x−60=0
x=−12 cm (nie należy dziedziny
lub x=5cm (należy do dziedziny
|BD}=2x=2*5=10cm
|AC|=2x+14=2*5+14=24cm
| |BD|*|AC| | 10*24 | |||
P= | = | =120cm2 | ||
| 2 | 2 |
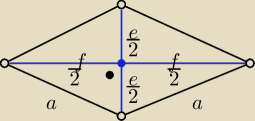
| fe | ||
P= | i f−e=14 | |
| 2 |
| fe | ||
49+ | =169 | |
| 2 |
| fe | ||
=P=120 cm2 | ||
| 2 |

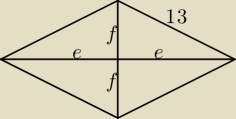 Tak samo, ale bez ułamków
e2 + f2 = 169 i pole P = 2ef, 2e − 2f = 14 ⇒ a − f = 7 ⇒ a2 − P + f2 = 49
stąd P = 169 − 49 = 120
Tak samo, ale bez ułamków
e2 + f2 = 169 i pole P = 2ef, 2e − 2f = 14 ⇒ a − f = 7 ⇒ a2 − P + f2 = 49
stąd P = 169 − 49 = 120