3 bardziej wymagające zadania, prosze o pomoc
Adam: pierwsze zadanie:
Punkty A=(1;2) B=(−1;0) C=(2;−2) są wierzchołkami trójkąta ABC.
a) napisz równania prostych w których zawierają się wysokości trójkąta ABC
b) oblicz obwód i pole tego trójkąta.
drugie zadanie:
Dany jest trójkąt o wierzchołkach M=(−2;1) N=(2;0) P=(2;5)
a) oblicz odległość punktu przecięcia się wysokości od wierzchołków trójkąta.
b) oblicz pole tego trójkąta
trzecie zadanie:
Boki trójkąta zawierają się w prostych o równaniach:
x+y−2=0 ; 3x−5y−14=0 ; x−y−2=0
a) oblicz współrzędne wierzchołków tego trójkąta.
b)napisz równanie okręgu opisanego na tym trójkącie.
29 maj 11:15
Adam: prosze o pomoc, te zadania sa naprawde trudne dla mnie
29 maj 12:01
Kate : postaram się ; )
29 maj 16:32
Kate :
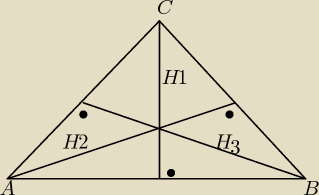
zad 1 .
a ) zauważ ,że wysokości spadają na dany bok pod kątem prostym, dlatego też, mają one
wspołczynniki przeciwne i odwrotne do prostej na którą spadaja .
tak więc :
wyznaczmy wysokość H
1 .
wsp.prostej AB : a
1 = 1 , dlatego wsp. wysokości H
1: a
2 = −1 i pkt C nalezy do prostej
zaiwerajacej wysokość H
1: y + 2 = −1(x−2) →
y = −x
wyznaczmy wysokość H
2 .
wsp.prostej BC : a
1 = −
23 , dlatego wsp. wysokości H
2 : a
2 =
32 i pkt A nalezy do
prostej zaiwerajacej wysokość H
2 : y−2 =
32(x−1) →
y = 32x +12
wyznaczmy wysokość H
3 .
wsp.prostej AC : a
1 = − 4 , dlatego wsp. wysokości H
3 : a
2 =
14 i pkt B nalezy do
prostej zaiwerajacej wysokość H
3 : y − 0 =
14(x+1) →
y = 14x + 14
29 maj 16:45
Kate : ciąg dalszy do a )
można to obliczyć ze wzoru Herona , by skorzystać z tego wzoru trzeba obliczyć długości
wszystkich boków trójkąta .
p − połowa obwodu
|AB| = 2√2
|BC| =√13
|AC| =√17
p = 12 ( AB| + |BC| + |AC| ) = ... oblicz to
a nastepnie wstaw do wzoru : √p(p−|AB|)(p−|BC|)(p−|AC|) = ...i otrzymasz pole .
29 maj 16:52
Eta:
witam
zad3/ rozwiąż układy trzech równań ( 1i 2 2 i 3 i 1 i 3 równanie)
otrzymasz współrzędne wierzchołków tego trójkąta.
policz zatem długości boków:
IABI , IACI , IBCI ( znasz wzór na długość odcinka)
Pole policz : np: ze wzoru Herona ( jak w przykładziea)
lub z wyznacznika pary wektorów np :
→ →
P=
12I d( AB, AC)I
29 maj 17:39