zadania dla chętnych
Eta: Zadanie dla chętnych
1/ Reszta z dzielenia wielomianu W(x) przez wielomian P(x)= x
4+2x
2−3
jest wielomianem R(x)=x
3−2x
2+x+2.
Wyznacz resztę z dzielenia wielomianu W(x) przez x
2−1
( podać najprostszy sposób rozwiązania zadania
15 gru 21:43
15 gru 21:44
Eta:
Hehe
15 gru 21:48
Trivial: Fajne zadanko. Nie podaję rozwiązania, żeby nie popsuć zabawy.
15 gru 21:48
Artur_z_miasta_Neptuna:
to ja też nie podaje
15 gru 21:51
Eta:
2/ Pewien student zapytany ile ma lat? odpowiedział:
jeżeli całkowitą liczbę moich lat pomnożymy przez liczbę o 50 mniejszą od liczby moich lat
i do wyniku dodamy 624 , to otrzymamy liczbę ujemną. Ile lat ma ten student?
15 gru 21:51
Maslanek: Wiele tych możliwości nie ma
15 gru 21:53
Eta:
3/ W prostokącie o przekątnej długości 12, połączono środki sąsiednich boków
otrzymując romb o kącie ostrym 60o.
Oblicz obwód i pole tego rombu.
15 gru 21:56
PW: Ad 2) Podejrzewam, że między 18 a 30. To się nazywa wstępna analiza danych.
15 gru 21:57
Eta:
4/ Wykaż,że istnieje tylko jeden trójkąt prostokątny, którego boki mają długości równe
kolejnym liczbom :
a) naturalnym
b) parzystym
15 gru 21:59
Eta:
@
PW
A może to student "trzeciego wieku" ?
15 gru 22:00
Saizou : a mi się wydaje że student będzie mieć 25 lat
15 gru 22:05
PW: Ciąg dalszy analizy danych: Za stary być nie może, bo po odjęciu 50 od jego wieku musimy
otrzymać liczbę ujemną.
Widzę, że już mi odbija. Pora spać
15 gru 22:07
Eta:
15 gru 22:16
Godzio:
Stawiam, że jest prostszy od tego
?
W(x) = Q(x)(x
2 + 3)(x
2 − 1) + x
3 − 2x
2 + x + 2
W(x) = G(x)(x
2 − 1) + ax + b
W(1) = 2 = a + b
W(−1) = − 2 = − a + b
b = 0
a = 2
R(x) = 2x
15 gru 22:17
Maslanek: Obwód: 24
Pole:18√3
15 gru 22:19
Eta:
Hej
Godzio .......... jasne,że jest
15 gru 22:20
Eta:
@
Maślanek ... napisz, który to nr. zadania
15 gru 22:21
tn: OK. A Możesz dać kilka z kombinatoryki ?
15 gru 22:22
Maslanek: 3 jak mniemam
15 gru 22:22
Eta:
Trudnych? czy łatwych?
15 gru 22:23
Saizou :
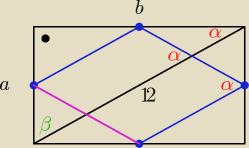
α=60
β=30
6
√3=a
b=6
zatem różowa (fioletowa) odległość ma długość =6
Ob=24
| | 1 | | √3 | |
P=2* |
| *6*6*sin60=36* |
| =18√3 |
| | 2 | | 2 | |
15 gru 22:24
Maslanek: Trudnych
15 gru 22:25
Eta:
zad3/ odp....ok
15 gru 22:25
tn: trudnych − poziom R matematyka liceum
15 gru 22:26
Saizou :
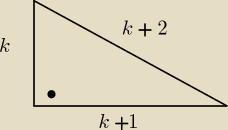
załóżmy że k∊N oraz k≠0
k
2+(k+1)
2=(k+2)
2
k
2+k
2+2k+1=k
2+4k+4
k
2−2k−3=0
Δ=4+12=16
√Δ=4
zatem istnieje jeden taki trójkąt o bokach 3,4,5
15 gru 22:31
tn: 4a)
n2 + n2+2n+1 − n2 − 4n − 4 = 0
n2 −2n −3 = 0
√Δ = 4
n1 = 3
n2 < 0 ∉D
Ale nie wiem jak rozważyć inną kolejność.
15 gru 22:32
tn: Ale może być też możliwość:
n2 + (n+2)2 = (n+1)2
15 gru 22:33
Saizou : niech n∊P i n>0
n
2+(n+2)
2=(n+4)
2
n
2+n
2+4n+4=n
2+8n+16
n
2−4n−12=0
Δ=16+48=64
√Δ=8
zatem istnieje taki trójkąt o bokach 6,8,10
15 gru 22:34
Saizou : tn ale wtedy nie będzie to trójkąt (trzeba uwzględnić nierówność trójkąta )
15 gru 22:35
tn: a nie zachodzi nierówność dla danych które pokazałem?
Bo sam się pogubiłem
15 gru 22:37
Eta:
dla
Saizou
15 gru 22:37
tn: Eta, to jak z tymi kombinatorycznymi ;> ?
15 gru 22:39
tn: Bo mi spać nie daje ta kombinatoryka
15 gru 22:39
Saizou : tn dla tego co pokazałeś jako pierwsze zachodzi nierówność
Eta dzięki za jabłuszko
15 gru 22:40
emu: Tak to czytam wszystko i mam jedno pytanie.Chce sie wam siedziec nad matma o prawie 23 w
weekend?
15 gru 22:40
tn: no właśnie, zachodzi, więc dlaczego tego nie uwzględniamy?
15 gru 22:40
Eta:
@
tn
Może jutro coś Ci wrzucę , bo dzisiaj już mi się nie chce
15 gru 22:40
tn: Wiesz, jakbyś miał maturę za 4 miesiące też byś siedział xd
15 gru 22:41
tn: Ok. To jutro zajrzę
15 gru 22:41
emu: Byc moze ,sorry ze tak wyjechalem z takim tekstem ,ale podziwiam was
15 gru 22:42
tn: Eta będziesz jeszcze chwilkę?
15 gru 22:42
Saizou : to tyczy się twojej alternatywnej wersji n2 + (n+2)2 = (n+1)2, w tym wypadku nie zachodzi ta
nierówność
15 gru 22:42
tn: Nic nie szkodzi za ten tekst
15 gru 22:42
Eta:
@
emu
Nad "matmą" ... można siedzieć : "do końca świata ... i jeszcze 1 dzień dłużej"
15 gru 22:42
Saizou : ja się na przykład relaksuję po dzisiejszym dniu (pierniki robiłem, kto chce
)− tak ok 500
szt.
15 gru 22:43
Eta:
Jaaaaaaaaaaaaaaaaaaaaaa chcę
( tylko lukrowane!
15 gru 22:44
Godzio:
A ja się ostatnio całe dnie relaksuje, po czym stwierdzam, że nic nie umiem i zaczynam się
uczyć wieczorami
15 gru 22:45
tn: Mam do Ciebie prośbę Eta
Czy pomożesz mi z kombinatoryką
Wiele czasu nie potrzebuję
15 gru 22:45
tn: Godzio nic nie umie.
Lepszej antytezy nie da się wymyślić
15 gru 22:45
Saizou : + posypka do tego
tu są ładnie zapakowane
15 gru 22:46
Eta:
@
tn ... postaram się
15 gru 22:46
krystek: I z posypką?
15 gru 22:46
emu: Ja z matmy kompletnie nie jestem kumaty ,wszedlem z nadzieja (byc moze glupia ) ze ktos za mnie
zrobi pare zadan na prace semestralna .Skonczylo sie na tym ,ze nic nie umiem ,zadan nie mam
,a stronka dalej otwarta i zagladam czasem
15 gru 22:46
Godzio:
Dzisiaj siedziałem 3 h nad całkami potrójnymi i chyba dalej ich nie opanowałem
15 gru 22:47
Eta:
Saizou tak zawiązałeś tę przesyłkę,że nie mogę jej rozpakować!
15 gru 22:47
tn: Ok. Dzięki wielkie
@Eta, a w liceum jest ona bardzo trudna ta kombinatoryka?
Bo dla mnie to najtrudniejszy dział w liceum, przy najmniej na razie dopóki nie ruszyłem
geometrii przestrzennej.
15 gru 22:47
Saizou : trzeba było mocno zawiązać żeby pierniki nie wypadły podczas transportu
15 gru 22:48
15 gru 22:48
tn: Nie bredzę, na prawdę trudne to jest
15 gru 22:49
Godzio:
Eta poziom jest taki, że nie wyrabiam się
Na uniwerku, algebra też jest kosmos, sporo
innych rzeczy niż na politechnice
Prosto nie jest
15 gru 22:50
Eta:
@
tn
To o "całki potrójne" pytasz? czy kombinatorykę?
15 gru 22:50
tn: Kombinatoryka⇒trudność⇒
15 gru 22:50
tn: Kombinatorykę
15 gru 22:50
Eta:
"wesołe jest życie .......... "studenta" haha
15 gru 22:51
tn: @Godzio a co studiujesz?
15 gru 22:51
tn: Ja tym studentem chciałbym już być ....
Nie wiem tylko czy podołam na informatyce, ale czas pokaże
15 gru 22:51
Godzio:
A co Godzio może studiować ;>
15 gru 22:51
Eta:
ukochaną matematykę
15 gru 22:52
tn: Matematykę
15 gru 22:52
Godzio:
15 gru 22:52
tn: @Eta, to wg CIebie jaka jest ta kombinatoryka w liceum?
Trudna czy łatwa czy średnia?
15 gru 22:53
tn: Godzio, a Ty też się znasz na kombinatoryce?
15 gru 22:53
Godzio:
Nie lubię kombinatoryki
Na zadaniu z kombinatoryki straciłem moje punkty na maturze
15 gru 22:54
Eta:
łatwo−średnia
( to przecież tylko jeden nowy dział)
15 gru 22:54
tn: Jak Godzio nie lubi, to jest przerażająca
Jutro Eta będziesz tutaj na forum ?
15 gru 22:55
Saizou : a wracając do zadań, jaki jest najłatwiejszy sposób na zadanie nr. 1
15 gru 22:56
Godzio:
Na mnie nie patrz
Po prostu mi nie podeszła
15 gru 22:56
Godzio:
Zrobione jest o 2217
15 gru 22:56
Eta:
zad1/ wystarczy podzielić R(x) przez x
2−1
lub tak jak pokazał
Godzio
15 gru 22:57
Saizou : ale chodzi o najprostszy sposób, post z 15 gru 2012 22:20
15 gru 22:58
Saizou : to dobrze myślałem
15 gru 22:59
Vizer: Ja bym temu studentowi w zadaniu 2 nie ufał, musiał być nawalony by coś takiego powiedzieć ....
15 gru 22:59
Eta:
15 gru 22:59
Eta:
Ejj
Vizer ? czy znasz tego studenta?
15 gru 23:00
Vizer: Może ..., ale nie będę wytykał palcami
15 gru 23:02
Eta:
15 gru 23:02
Saizou : a ten student ile ma lat
15 gru 23:11
Eta:
?
15 gru 23:12
Eta:
22:05
15 gru 23:13
Saizou : czyli jednak dobrze
15 gru 23:14
Vizer: Nie wiem właściwie, cały czas nawalony chodzi ... i nie ma kiedy go spytać, ale jak tylko
wytrzeźwieje dam Wam znać !
15 gru 23:14
Mila:
tn nie bój się kombinatoryki.Na maturze są typowe zadania.
emu sprawdzaj swoje zadania.
Saizou, dobrze się sprawiasz.
Eto, ładne zadanka.
16 gru 00:19
tn: To jak będzie z tymi kombinatorycznymi
?
16 gru 16:24