Nierownosc emu: Mogłbym prosic kogos o rozwiazanie tego?Dziekuje z gory.

x+2		x+3		2
	≤		+
x−2		x−3		x2−5x+6

Artur_z_miasta_Neptuna: 1) założenia 2) wspólny mianownik 3) wszystko na jeden ułamek 4) mnożysz przez kwadrat mianownika (wtedy mnożysz przez która na pewno jest liczbą dodatnią) 5) metoda 'wężyka'

ewelina: jak się mylę proszę poprawić

	x+3		2		x+2		2
0≤		+		+		/:
	x−3		x2−5x+6		x−2		x2−5x+6

	x+3		x2−5x+6		x+2		x*2−5x+6
0≤		*		−		*
	x−3		2		x−2		2

	(x+3)*(x2−x5+6)		(x+2)*(x2−5x+6)
0≤		−		skracamy i mamy wspólny mianownik
	2(x−3)		2(x−2)

	x2−5x+6		x2−5x+6
0≤		+		/*(−1)
	−2		−2

	x2+x2−5x−5x+6+6
0≤
	2

	2x2−10x+12
0≤
	2

0≤x²−5x+6

emu: Liczba "2" jest pierwiastekiem podwojnym wielomianu W(x)=x³−x²+px+q a)Oblicz wspolczynniki p i q b)wyznacz pozostale pierwiastki wielomianu W(x)

ewelina: Δ=b²−4*a*c Δ=5²*4*1*6 Δ=25−24 Δ=1

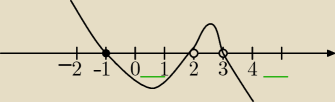Mila: Sposób Eweliny jest błędny. Nie wolno mnożyć nierówności przez wyrażenie o nieznanym znaku. x²−5x+6=0⇔Δ=1 ;x₁=2; x₂=3 zał. x≠2 i x≠3

x+2		x+3		2
	−		−		≤0⇔
x−2		x−3		(x−2)(x−3)

	(x+2)(x−3)		(x+3)(x−2)−2
		−		≤0
	(x−2)(x−3)		(x−2)(x−3)

x2−3x+2x−6−(x2−2x+3x−6)−2
	≤0
(x−2)(x−3)

−2x−2)
	≤0⇔2(−x−1)(x−2)(x−3)≤0⇔
(x−2)(x−3)

x∊<−1;2)∪(3;∞)

Mila: W(x)=x³−x²+px+q x=2 jest pierwiastkiem podwójnym w(2)=0 i (x−2)²*(x−a)=x³−x²+px+q⇔ spróbuj dokończyć.