Koła i okręgi karmazynowy msciciel: Zadanie dla prawdziwych twardzieli: Dane są dwa okręgi styczne zewnętrznie w punkcie A i prosta k, będąca styczną jednocześnie do tych dwóch okręgów odpowiednio w punktach B i C. Uzasadnij, że środek odcinka BC leży w takiej samej odległości od punktu A, jak od punktów B i C.

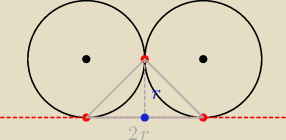
Artur_z_miasta_Neptuna: zapomniałeś (chyba) dodać, że okręgi są jednakowych promieni.

karmazynowy msciciel: Niestety, nie zapomnialem zadanie słowo w słowo przepisane z książki, a jeśli nie piszę, że dwa są jednakowe zadanie nie jest takie proste

Artur_z_miasta_Neptuna: pomysł nr1 wykazać że AD leży na stycznej do tych dwóch okręgów (prosta styczna w punkcie A) z tego wynika, że AD prostopadła do promieni... z proporcji małych trójkątów wynika, że y=x

PW: Wystarczy pokazać, że prosta PA jest styczna do obu okręgów. (P to środek BC).

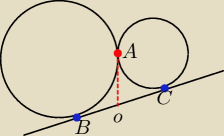
MQ: wybieramy taki punkt na prostej BC, że: prosta AO jest styczna do dużego okręgu i prosta AO jest styczna do małego okręgu ale ponieważ O leży na BC, więc: prosta BO jest styczna do dużego okręgu prosta CO jest styczna do małego okręgu z symetrii problemu mamy: AO=BO oraz AO=CO więc: BO=CO

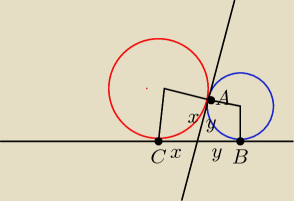
PuRXUTM: ja chyba wiem... z twierdzenia o odcinkach stycznych ( chyba tak to się nazywa...) x=y

Jeevan: Podpowiem, że trzeba skorzystać z faktu, że: Dowolny kąt wpisany oparty na półokręgu (czyli oparty na średnicy) jest kątem prostym tzn. ma miarę 90°