zbadaj monotonicznosc ciagu krychadd: zbadaj monotonicznosc ciagu : a = 3−2n² n

Damian: POMAGAM

Damian: a_n = 3 − 2n² a_n+1 = 3 −2(n+1)² = 3 − 2(n² +2n+1) = 3 −2n² + 4n +2 = 5 −2n² + 4n sprawdzam monotoniczność: a_n+1 − a_n = 5 −2n² + 4n − (3 − 2n²) = 5 −2n² + 4n −3 + 2n² = 4n + 2 4n+2 > 0 wiec ciąg jest roznącym ponieważ n ∊ N

Eta: Witam Do znudzenia tego typu zadań na tym forum badamy znak różnicy a_n+1 − an gdzie n€N jezeli >0 −−− c. rosnący <0 −−c. malejący =0 −− c. stały a_n+1= 3 − 2( n+1)² = 3 −2n² −4n −2 = −2n² −4n +1 więc: a_n+1 − a_n = −2n² −4n +1 − 3 +2n²= −4n −2 <0 bo n€N więc c. jest malejący ..........co widać gołym okiem

Eta: Damian ...... i co ...... gołym okiem widać ,że malejący Znalazłeś bład?

Damian: wiem ... ma być −4n przepraszam za znaki

Damian: nie pomnożyłem przez −2 tylko przez 2 i znaki sie poten tego wały...

matematyczny retard: a_n=n²−4n+3 Dlaczego badając monotoniczność zgodnie z a_n+1 − a_n wychodzi 1, a ciąg nie jest rosnący? Żle liczę, czy robię jakieś błędne założenia, bo pierwsze wyrazy ciągu to 0, −1, 0 (n²−4n+3)+1 − (n²−4n+3) = n²−4n+4−n²+4n−3 = 1

matematyczny retard: Już nieważne − jestem debilem

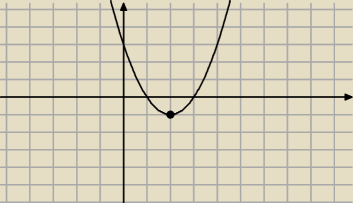
Krzysiek60 : ten ciag nie jest monotoniczny jest monotoniczny w przedzialch

Krzysiek60 : Nie obrazaj sie . Przeczytaj definicje debila .