stereometria .: Ostrosłup prawidłowy trójkątny o podstawie ABC i wierzchołku S przecięto płaszczyzną przechodzącą przez środki krawędzi AC, BC, AS, BS. Pole otrzymanego w ten sposób przekroju jest 4 razy mniejsze od pola powierzchni bocznej tego ostrosłupa. Oblicz cos kata nachylenia ściany bocznej do płaszczyzny podstawy. Proszę o pomoc

.: ?

.: nikt nie umie? jakaś wskazówka chociaż. proszę

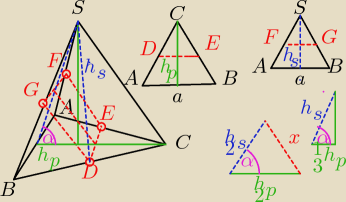
dero2005: oznaczenia h_p − wysokość podstawy h_s − wysokość ściany a − bok podstawy DEFG − prostokąt przekroju FE = DG = x z trójkąta ABC

hp		hP   2		a
	=		⇒ DE =
a   2		DE   2		2

z trójkąta ABS

hs		hs   2		a
	=		⇒ FG =
a   2		FG   2		2

P_p = pole przekroju DEFG

	a
Pp = DE*DG =		*x
	2

P_b = pole boczne ostrosłupa

	3
Pb =		a*hs
	2

z warunków zadania 4*P_p = P_b czyli

	a		3
4*		*x =		a*hs
	2		2

	3
x =		hs
	4

trójkąt niebiesko−zielono−czerwony (twierdzenie cosinusów) x2 = (hs2)2 + (hp2)2 − 2*hs2hp2*cosα

	3		hs2		hp2		hs*hp
(		hs)2 =		+		− 2		*cosα
	4		4		4		4

9		hs2		hp2		hs*hp
	hs2 =		+		−		*cosα |*16
16		4		4		2

9h_s² = 4h_s² + 4h_p² − 8h_s*h_p*cosα 5h_s² = 4h_p² − 8h_s*h_p*cosα teraz rozpatrujemy trójkącik po prawej stronie (zielono−zielono−niebieski)

hp   3
	= cosα ⇒ hp = 3cosαhs
hs

wstawiamy to do poprzedniego wzoru 5h_s² = 1(3*cosα*h^s)² − 8h_s*3cosαh_s*cosα 5h_s² = 36cos²αh_s² − 24h_s²cos²α 5h_s² = 12cos²αh_s² |: h_s² 5 = 12cos²α

	5
cos2α =
	12

	√15
cosα =
	6

sprawdź te obliczenia

dero2005: korekta: wzór po słowach poprzedniego wzoru 5h_s² = 4(3*cosαh_s)² − 8h_s*3cosα*h_s*cosα

.: Dziękuję bardzo!

Mila: Brawo dla Dero. Wynik:x− taki sam, ale dalej inaczej liczyłam

	√15
cosα=
	12

Czy może masz odpowiedź?