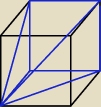
 W sześcianie o krawędzi długości 3 wszystkie wierzchołki jednej ściany połączono z jednym
wierzchołkiem ściany równoległej. Oblicz objętość otrzymanego ostrosłupa.
Wnioski:
Podstawa ostrosłupa ma krawędź długości 3. Ostrosłup ma jedną krawędź będącą przekątną bryły o
długości 3√3 oraz dwie krawędzie o długości 2√2 i pięć o długości 3. Czyli podstawa ma
pole równe 9. Wysokość obliczam z trójkąta o bokach [a, b, c][√2, h, 3√3] z Tw. Pitagoras
W sześcianie o krawędzi długości 3 wszystkie wierzchołki jednej ściany połączono z jednym
wierzchołkiem ściany równoległej. Oblicz objętość otrzymanego ostrosłupa.
Wnioski:
Podstawa ostrosłupa ma krawędź długości 3. Ostrosłup ma jedną krawędź będącą przekątną bryły o
długości 3√3 oraz dwie krawędzie o długości 2√2 i pięć o długości 3. Czyli podstawa ma
pole równe 9. Wysokość obliczam z trójkąta o bokach [a, b, c][√2, h, 3√3] z Tw. Pitagoras
| 1 | ||
h = 5. Czyli objętość zaznaczonego na niebiesko ostrosłupa jest równa | 9*5 = 15 [j3]? | |
| 3 |
| 1 | 1 | |||
V= | Pp*H= | *(3*3)*3=9[j3] moim zdaniem, ale mogę się mylić | ||
| 3 | 3 |
 .
.
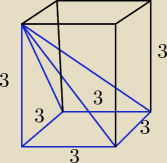 popatrz na to zadanie, na ten rysunek z innej strony
Po prostu nie trzeba nic liczyć, tylko odczytać
popatrz na to zadanie, na ten rysunek z innej strony
Po prostu nie trzeba nic liczyć, tylko odczytać 