ptosta i punkty lui: Na płaszczyźnie dane są punkty A=(3,−2) i B=(11,4). Na prostej o równaniu y=8x+10 znajdź punkt P, dla którego IAPI²+IBPI² jest najmniejsza.

MQ: IAPI²+IBPI²=(x−3)²+(y+2)²+(x−11)²+(y−4)² Za y podstawiasz 8x+10 Dostajesz równanie na jakąś funkcję f(x). Szukasz minimum tej funkcji. Dostajesz x. Z równania prostej wyliczasz y.

Gustlik: Jak MQ, otrzymasz funkcję kwadratową, minimum to współrzędne wierzchołka paraboli p i q. Oblicz p i to p to jest Twoje x, a y obliczysz wstawiając ten x do równania prostej.

PW: Z twierdzenia cosinusow mniej rachunkow (suma kwadratow najmniejsza, gdy cos∡(PA^→,BP^→) = 0 (iloczyn skalarny wektorow jest rowny zeru)

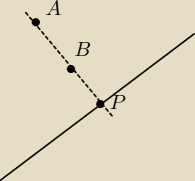MQ: @PW taki przykład −− co ty na to?

PW: Wtedy dla żadnego punktu prostej iloczyn skalarny nie będzie zerem i trzeba wyciągnąć wnioski.. Uprzejmie donoszę, że nie rozwiązywałem zadania, a podpowiadałem tylko inną możliwość − do twórczego rozwinięcia.

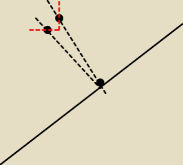MQ: @PW a teraz?

lui: właśnie wróciłam do tego zadania, okazało się że rozwiązywałam metodą MQ ale (jak to u mnie często bywa) wkradł mi się błąd rachunkowy i źle mi wychodziło odp. P=(−1,2) dziękuję bardzo za pomoc