Dla jakich wartości parametru m równanie ma 2 różne rozwiązania. demi: Dla jakich wartości parametru m równanie ma 2 różne rozwiązania. (m+2)x² − 2x + m + 2 = 0 PS: Macie może rozwiązania do zbioru zadań z matematyki (zakres podstawowy i rozszerzony kl.2) Krzysztofa Kłaczkowa?

loitzl9006: Dwa warunki: 1 − delta większa od zera, a także 2 − współczynnik przed x² ma być niezerowy Miałem ale opchnąłem − teraz żałuję, trochę by się przydał taka czerwona okładka − chyba o to Ci chodzi?

ZKS: Jak coś ja mam.

demi: ZKS mógłbyś wysłać link do pobrania?

ZKS: Ale to chcesz żeby Ci zeskanować?

demi: BTW nie chodzi mi o te rozwiązania co z tyłu są, bo te mam, tylko o rozwiązane zadania krok po kroku w jakimś zeszycie.

ZKS: Więc na łatwiznę chcesz iść?

demi: Nie do końca, zdaję maturę podstawową, ale mamy taką nauczycielkę co ciśnie i wymaga od nas zadań z rozszerzenia, bo mówi, że może akurat ktoś się pokusi o rozszerzenie. Jakbyś miał to bardzo bym prosił. Nie musiałbym się dopytywać o konkretne przykłady za każdym razem.

ZKS: Zeszyt zanim bym znalazł to Ty już dawno będziesz po maturze (możliwe że nawet go wyrzuciłem bo po co mi by był potrzebny).

demi: Ok, tak czy siak dzięki za fatygę. Spróbuje samemu porobić te zadania.

ZKS: loitzl9006 podał warunki do zadania więc na pewno dasz radę. Jeżeli będziesz chciał sprawdzić odpowiedź napisz to ktoś Ci sprawdzi.

demi: Wyszła mi delta −4m² − 16m −12 Co dalej?

Artur_z_miasta_Neptuna: a skąd taka Δ

Artur_z_miasta_Neptuna: przecież masz podane warunki zadania ... masz zbadać dla jakiego 'm' zachodzi: Δ>0 i jednocześnie a≠0

demi: (m+2)x2 − 2x + m + 2 = 0 a różne od 0, czyli m ≠ −2 Δ > 0 Δ = b² − 4ac Δ = 4−4((m+2)(m+2)) Δ = 4−4m² − 16m − 16 Δ= −4m² − 16m − 12 Stąd mam deltę i co teraz?

ZKS: Teraz warunek Δ > 0. Masz obliczone Δ = −4(m² + 4m + 3) więc to wstawiamy i mamy −4(m² + 4m + 3) > 0 rozwiąż tą nierówność.

demi: m ∊ (−3,−2) u (−2,−1) To jest rozwiązanie. Mógłby ktoś pokazać jak do niego dojść rozwiązując nierówność w delcie? Wiem, że (m2 + 4m + 3) można przedstawić jako (m+3)(m+1) i stąd mamy msc. zerowe, ale jakoś inaczej, bardziej "profesjonalnie" da się to rozwiązać?

Gustlik: Ja mam ten zbiór.

demi: A szczegółowe rozwiązania do niego?

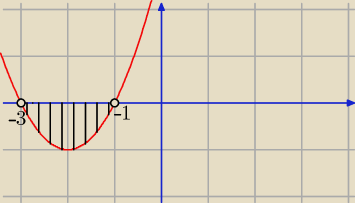
ZKS: Zaznaczasz na osi miejsca zerowe i rysujesz parabolę a > 0 więc parabola ramionami skierowana do góry. Mamy znaleźć takie argumenty dla których wartości funkcji są mniejsze od 0. Naszym rozwiązaniem jest x ∊ (−3 ; −1) ale mamy jeszcze warunek że a ≠ 0 ⇒ m ≠ −2 więc należy to uwzględnić ostatecznie otrzymujemy x ∊ (−3 ; −1) \ {−2}.

ZKS: Gustlik wyżej napisałem że ja mam ten zbiór ale koledze chodzi o pełne rozwiązania.

ZKS: Wyjaśnię dlaczego ja mam a > 0 bo może być nie jasne skoro −4m² − 16m − 12 > 0? Otóż wyłączyłem wspólny czynnik przed nawias a więc −4 i otrzymałem −4(m² + 4m + 3) > 0 podzieliłem obustronnie przez −4 zmieniłem zwrot nierówności na przeciwny dostając m² + 4m + 3 < 0 wyżej narysowany wykres funkcji właśnie obrazuję tą nierówność.