proszę o pomoc monika: zad 1. Punkty A=(0,−2) i B=(4,4) są wierzchołkami trójkąta równobocznego ABC. a) Oblicz pole P trójkąta ABC. b) Napisz równanie prostej zawierającej wysokość trójkąta poprowadzoną z wierzchołka C. c) Wyznacz współrzędne wierzchołka C. zad 2. Punkty B=(5,6) i D=(−1,3) są końcami jednej wysokości trójkąta równobocznego. a) Napisz równanie okręgu wpisanego w ten trójkąt, wiedząc że punkt D nie jest wierzchołkiem trójkąta b)Oblicz współrzędne pozostałych wierzchołków tego trójkąta zad 3. Oblicz pole P trójkąta, którego wierzchołkami są środki okręgów o równaniach x²+y²+4x−2y−15=0 i x²+y²−4x+2y−5=0 oraz punkt A przecięcia się prostych o równaniach x+2y−5=0 i 3x−y+1=0

Artur_z_miasta_Neptuna: krok 1 ... narysuj układ współrzędnych i zaznacza punkt A i B krok 2 ... wyznaczasz środek odcinka AB oraz długość odcinka AB krok 2a ... z doskonale znanego Ci wzoru obliczasz pole trojkąta równobocznego (podpunkt a) krok 3 ... wyznaczasz prostą prostopadłą do odcinka AB przechodzącą przez środek tego odcinka (wyznaczony w kroku 2) (podpunkt b) krok 4 ... z doskonale Ci znanego wzoru na wysokość w trojkącie równobocznym wyznaczasz wysokość tego trójkąta krok 5 ... wyznaczasz dwa możliwe położenia punktu C na prostej wyznaczonej w kroku 3 ... takie, aby odległośc punktu C od środka odcinka AB (krok 2 i 3) wynosiła tyle ile wynosi wysokość trójkąta (punkt 4) (podpunkt c) krok 6 ... koniec zadania

Artur_z_miasta_Neptuna: zad 2 ... analogicznie

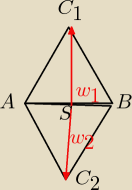
Gustlik: Z wektorów: A=(0,−2) B=(4,4) ad a) AB^→=[4−0, 4−(−2)]=[4, 6] dł. boku a=|AB|=√4²+6²=√16+36=√52=2√13

	a2√3		(2√13)2*√3		52√3
Pole =		=		=		=13√3
	4		4		4

ad b) Współczynnik kierunkowy AB:

	6		3
a1=		=		(dzielę współrzędną y wektora AB→ przez jego współrzędną x)
	4		2

Pr. AB:

	3
y=		x+b
	2

	3
−2=		*0+b
	2

b=−2

	3
y=		x−2
	2

	3
0=		x−y−2
	2

3
	x−y−2=0/*2
2

3x−2y−4=0 Kazdy wektor o współrzędnych [kA, kB] jest prostopadły do prostej Ax+By+C=0 Wektor prostopadły do tej prostej: w^→=[3k, −2k] jego długość: |w|=√(3k)²+(−2k)²=√9k²+4k²=√13k²=√13|k| musi być równa wysokości trójkąta:

	2√13*√3
h=U{a√3{2}=		=√39
	2

czyli √13|k|=√39 /:√13 |k|=√3 k₁=√3 v k₂=−√3 Wektor w₁^→=[3√3, −2√3] v w₂^→=[−3√3, 2√3] A=(0,−2) B=(4,4) Środek AB:

	0+4		−2+4
S=[		,		)=(2, 1)
	2		2

wektor w^→=SC^→=C−S ⇒ C=S+SC^→ C₁=(2, 1)+[3√3, −2√3]=(2+3√3, 1−2√3) C₂=(2, 1)+[−3√3, 2√3]=(2−3√3, 1+2√3)

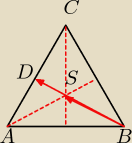
Gustlik: zad 2. Punkty B=(5,6) i D=(−1,3) są końcami jednej wysokości trójkąta równobocznego. a) Napisz równanie okręgu wpisanego w ten trójkąt, wiedząc że punkt D nie jest wierzchołkiem trójkąta b)Oblicz współrzędne pozostałych wierzchołków tego trójkąta: Liczę współrzedne wektora BD^→ i jego długość, czyli wysokość Δ. B=(5,6) D=(−1,3) BD^→=[−1−5, 3−6]=[−6, −3] h=|BD|=√(−6)²+(−3)²=√36+9=√45=3√5

	1
Promień okręgu wpisanego r=		h=√5
	3

	2		2
Liczę współrzędne wektora BS→=		*BD→=		*[−6, −3]=[−4, −2]
	3		3

BS^→=S−B ⇒ S=B+BS^⇒ S=(5, 6)+[−4, −2]=(5−4, 6−2)=(1, 4) jest to środek okręgu. Okrąg ma równanie: (x−1)²+(y−4)²=5 ad b) Oblicz współrzędne pozostałych wierzchołków tego trójkąta:

	xA+xC		yA+yC
S=SAC=(		,		)=(−1, 3)
	2		2

	xA+xB+xC
S=(		, yA+yB+yC}{3})
	3

	xA+5+xC
S=(		, yA+6+yC}{3})=(1, 4)
	3

Rozwiąż teraz układy równań − otrzymasz współrzędne wierzchołków:

	xA+xC
{		=−1
	2

	xA+5+xC
{		=1
	3

oraz

	yA+yC
{		=3
	2

{ y_A+6+y_C}{3})=4

Gustlik: zad 3. Oblicz pole P trójkąta, którego wierzchołkami są środki okręgów o równaniach x2+y2+4x−2y−15=0 i x2+y2−4x+2y−5=0 oraz punkt A przecięcia się prostych o równaniach x+2y−5=0 i 3x−y+1=0 x²+y²+Ax+By+C=0

	A
a=−
	2

	B
b=−
	2

r=√a²+b²−C, r>0 x2+y2+4x−2y−15=0

	4
a=−		=−2
	2

	−2
b=−		=1
	2

A=(−2, 1) x2+y2−4x+2y−5=0

	−4
a=−		=2
	2

	2
b=−		=−1
	2

B=(2, −1) { x+2y−5=0 { 3x−y+1=0 { x+2y=5 { 3x−y=−1 /*2 { x+2y=5 { 6x−2y=−2 + −−−−−−−−−−−−−−−−−−−−− 7x=3 /:7

	3
x=
	7

3
	+2y=5 /*7
7

3+14y=35 14y=35−3 14y=32 /:14

	32		16
y=		=
	14		7

	3		16
C=(		,
	7		7

Masz wierzchołki Δ A=(−2, 1) B=(2, −1)

	3		16
C=(		,
	7		7

Ciąg dalszy z wyznacznika wektorów − wskazówka tutaj w moich postach: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3423