Geometria analityczna
PuRXUTM: prosta o równaniu x+y−2 jest osią symetrii trójkąta równoramiennego ABC (|AC|=BC|), w którym
A=(−3,−1). Wiedząc, że przez punkt C przechodzi prosta o równaniu 2x+y+1=0 wyznacz współrzędne
wierzchołków B i C. Oblicz pole koła opisanego na tym trójkącie.
Proszę tylko o sprawdzenie odpowiedzi:
B=(3,5) C=(−3;5) P=18π
14 gru 23:30
Artur_z_miasta_Neptuna:
PuR ... daj obliczenia lub chociaż rysunek ... bo szczerze mówiąc −−− w pamięci tego nie
zrobię ... a jest za późno abym to rozpisywał ... z góry dziękuję
14 gru 23:32
PuRXUTM: obliczeń mam na 1,5 str A4 tak że szczerze mówiąc nie chce mi się tego przepisywać, jak nie
masz ochoty nikt Cię, nie zmusza do tego żebyś to robił, są jeszcze inni więc może ktoś będzie
chciał obliczyć...
14 gru 23:35
Artur_z_miasta_Neptuna:
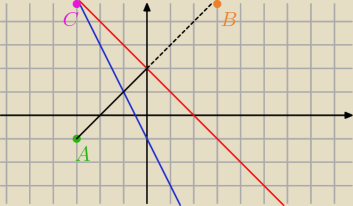
masz dobrze punkty ... okrąg opisany jest o promieniu r=3
√2 ... czyli wszystko dobrze
14 gru 23:53
Artur_z_miasta_Neptuna:
to sporo tych obliczeń masz
14 gru 23:53
Eta:
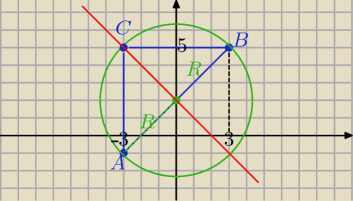
Wystarczyło umieścić ten trójkąt w układzie współrzędnych ( i masz sprawdzenie)
R= 3
√2
czyli odp: ok
14 gru 23:57
15 gru 13:57
