geometria analityczna
Black_Batty: | | 1 | | 1 | |
Punkty A(a,0), B(0,− |
| ), C(0,−2 |
| ) są wierzchołkami trójkąta o polu równym 18, jeśli |
| | 4 | | 2 | |
A.|a|=32 B.|a|=18 C.|a|=16 D.|a|=12
14 gru 23:14
PuRXUTM: ja bym podstawił do wzoru na pole
| | 1 | |
P= |
| |(xb−xa)(yc−ya)−(yb−ya)(xc−xa)| i powinno wyjść  |
| | 2 | |
14 gru 23:20
Eta:
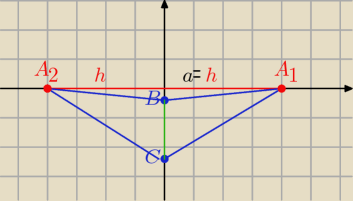
| | |AB|*h | | 1 | | 1 | |
P= |
| = 18 ⇒ P= | 2 |
| − |
| |* |a|}=2*18 |
| | 2 | | 2 | | 4 | |
|a|= .......... = 16
14 gru 23:24
14 gru 23:25
PuRXUTM: Eto a nie lepiej z tego mojego wzoru ?
14 gru 23:36
Eta:
Dla mnie ... nie

14 gru 23:58


