Wartość Bezwzględna.Parametr.F.kwadratowa.Równanie. V: Rozwiąż równanie 2x²−|5x|−m=0. Podaj ile jest rowiązań w zależności od parametru m. Dlaczego jak robię dwa przypadki dla x≥0 lub x<0 i liczę Δ>0 lubΔ=0 lub Δ<0 to mi nie wychodzi?

Maslanek: Bo to bez sensu Zrób w ten sposób 2x²−|5x|−m=0 2|x|²−5|x|−m=0 Niech |x|=t; t≥0. Wtedy 2t²−5t−m=0 Dalej samemu Kiedy t=0, to mamy jedno rozwiązanie x=0.

V: 1.dlaczego zrobiłeś wstawiłeś za x² −−> |x| ? 2. dlaczego bez sensu ?

V: Ja to mam z wykresu policzone, ale po to wstawiam to zadanie, aby ktoś mi wyjaśnił, dlaczego ta metoda jest błędna, a przy okazji dlaczego można podstawić za x² == |x|

V: Hej! Naprawdę proszę o chwilkę uwagi.

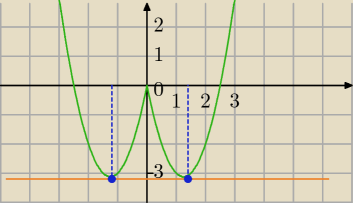
Mila: Rozwiązujemy graficznie: 2x²−|5x|−m=0 ⇔2x²−5|x|=m f(x)=2x²−5|x| i y=m

	5
xw=		dla funkcji y=2x2−5x
	4

	5
i xw=−		dla funkcji y=2x2+5x
	4

	25		5		1
yw=2*		−5|−		|=−3
	16		4		8

rysujesz y=m prosta pozioma ( funkcja stała)

	1
Dla m<−3		brak rozwiązań
	8

	1
dla m=−3		dwa rozwiązania (zaznaczyłam na niebiesko)
	8

	1
dla m∊(−3		;0) cztery rozwiązania
	8

dla m=0 trzy rozwiazania dla m>0 dwa rozwiązania

V: Dzięki Mila, ale dlaczego nie mogę tego rozwiązać w taki sposób, jak podałem− dlaczego to jest "bez sensu"? I dlaczego wolno mi zrobić coś takiego jak x² −−>|x| ? ? ? Proszę

Mila: Nic takiego nie powiedziałam, że bez sensu. Tylko trudniej rozwiązać algebraicznie. Trzeba rozważyć przypadki I) x≥0 2x²−5x−m=0 Δ=25+8m

	−25
a) Δ<0 brak rozwiązań⇔25+8m<0⇔8m<−25⇔m<
	8

	−25
b) Δ=0jedno rozwiązanie ⇔m=
	8

i tak musisz rozważyć do końca wszystkie przypadki i połączyć.

pigor: ... nikt "nie chce'' ci odpowiedzieć dlaczego |x|²=x² , no to może ja powiem tak : z definicji modułu (w.b) masz |x|=x gdy x≥0 lub |x|=−x gdy x<0 ⇒ |x|²=(±x)⁼ x² i tyle . ...

V: Dzięki pigor Mila, rozpatruję ale w ten sposób jakoś gubi mi się m=0, trzeba rozpatrzeć osobno ?

Mila: Dlatego, należy skorzystać z wykresu.

PW: A gdyby tak oderwać się od schematu "dwie parabole na dwóch półosiach"? Popatrzmy na to zadanie tak (jest to inne opowiadanie o sposobie pigora) 2x² − m = |5x| Na rysunku będzie parabola y=2x² przesunięta o (−m) i "dzióbek" y=|5x| Funkcje po obu stronach są parzyste, więc możemy rozwiązać równość tylko dla x≥0 (a drugie rozwiązania będą "takie same tylko że ujemne" − tego nie pisać w pracach maturalnych). 2x² − m = 5x, x∊<0.∞) 2x²−5x−m=0, x∊<0.∞)