Rozwiaz nierownosc wymierna z wartoscia bezwzgledna Wasylek: Rozwiaz nierownosc wymierna z wartoscia bezwzgledna |x+2| −−−−−− > 3 |x−1|

Mati_gg9225535: Dziedzina a potem 2 przypadki

Wasylek: Dziedzine mam R\{1.} Ale jak dalej ?

Mati_gg9225535: w sumei to 4 przypadki, 1. |x+2|≥0 i |x−1|≥0 2. |x+2|≥0 i |x−1|<0 3. |x+2|<0 i |x−1|≥0 4. |x+2|<0 i |x−1|<0 i do każdego obliczasz osobno tę nierownosc pamietajac o zmianie znaku gdy jest <0

Mila: |x+2|>3|x−1| i x≠1 a) x+2≥0⇔x≥−2 b)x−1>0⇔x>1 przedziały:(−∞;−2)∪<−2;1)∪(1;∞) 1)x∊(−∞;−2) obydwa wyrażenia są ujemne |x+2|>3|x−1|⇔−x−2>3*(−x+1) −x−2>−3x+3

	5
2x>5⇔x>		brak rozw. w podanym przedziale
	2

2)x∊<−2;1)

	1
x+2>3(−x+1)⇔x+2>−3x+3⇔4x>1⇔x>
	4

	1
x∊(		;1)
	4

3)x∊(1;∞) x+2>3(x−1)⇔x+2>3x−3⇔5>2x⇔x<2,5

	1
odp.x∊(		;1)∪(1;2,5)
	4

PW: A leniwy może poszukać mniej kłopotliwego rachunkowo sposobu. Zauważmy, że licznik lewej strony jest o 3 weiększy od mianownika dla wszystkich x∊R\{1}, a więc podstawiając u=x−1 otrzymamy nierówność

	|u+3|
(*)		>3, u∊R\{0}
	|u|

	u+3
|		|>3
	u

	3
|1+		|>3,
	u

a to oznacza, że

	3		3
1+		< −3 lub 1+		> 3
	u		u

	3		3
(**)		< −4 lub		> 2
	u		u

Pierwsza nierówność nie może być spełniona dla u>0 (ułamek o liczniku i mianowniku dodatnim jest dodatni), szukamy więc rozwiązań w zbiorze u∊(−∞,0). Po pomnożeniu obu stron nierówności przez u j e m n e u dostajemy

	3		3
3 > −4u, u<0 ⇔ −		< u ⇔ u∊(−		,0).
	4		4

Druga z nierówności (**) może być spełniona tylko dla u>0, a więc po pomnożeniu przez d o d a t n i e u dostajemy

	3
3 > 2u, u∊(0,∞) ⇔ U(3}{2} >u, u∊(0,∞) ⇔ u∊(0,		)
	2

	3		3
Tak więc rozwiązaniem nierówności są u∊(−		,0)∪(0,		).
	4		2

Po powrocie do podstawienia u=x−1 widzimy, że zadana nierówność jest spełniona dla takich x, dla których

	3		3		1		5
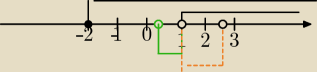
x−1 ∊(−		,0) lub x−1 ∊(0,		), to znaczy x ∊ (		,1) lub x∊(1,		).
	4		2		4		2

Ktoś może powiedzieć, że takie rozwiązanie wcale nie jest łatwiejsze. Pokazuję je głównie dlatego, żeby zwrócić uwagę, że w niektórych zadaniach można odejść od sztampy "rozbijania na przedziały". Jest to żmudne, a większość uczniów przeraża już na samym wstępie. Dla zabawy popatrzmy na takie zadanie: Udowodnij, że dla x∊R prawdziwa jest nierówność |x+9|+|x+4| > 4. Działający rutynowo rozbije rozważania na trzy przedziały i rozwiąże trzy nierówności. Działając nietypowo możemy zauważyć: prawdziwa jest nierówność |a|+|b| ≥ |a−b| (dla dowolnych a i b). Biorąc a=x+9 i b=x+4 dostaniemy |x+9|+|x+4|≥ |x+9−(x+4)| = |5| >4 Koniec dowodu − w jednej linijce!