funkcja wykładnicza Iks: Rozwiąż nierówności: a) 0,5^x+0,5^x+1+0,5^x+2+...>2√(¹₂)^x+2 b) 2^−cosx+4^−cosx+8^−cosx+...≤1 Prosze o pomoc

krystek: a) wyłacz0,5^x i zostaje Tobie suma nieskończonego c geomert

Iks: coś nie wychodzi... 0,5^x(1+0,5+0,5²+...) S=^0,5x_1−0,5=2*0,5^x 2*0,5^x>2√(¹₂)^x+2 0,5^2x>(¹₂)^x+2 (¹₂)^3x>2 wychodzi mi x<−¹₃ powinno byc x<−1

Iks: ?

Mila:

	1
S=		=2
	1−0,5

	1
L=2*(		)x
	2

	1
2*(		)x>2√0,5)x+2 /:2
	2

	1
(		)x>√0,5)x+2 /2
	2

	1		1
(		)2x>(		)x+2}
	2		2

1
	)x=t i t>0
2

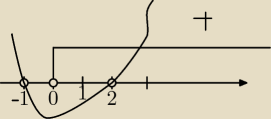
t²−t−2>0 i t>0 Δ=9

	1−3		1+3
t1=		=−1 lub t2=		=2
	2		2

(t+1)(t−2)>0 i t>0⇔t>2

	1
(		)x>2⇔2−x>21⇔−x>1⇔x<−1
	2

Jasiu: Jeżeli chodzi o drugie zadanie to wydaja mi sie tak:

	1		1		1
(		)cosx +(		)cosx+(		)cosx+...≤1
	2		4		8

gdyby cosx <0 to wtedy całość byłaby napewno większa od 1 dla cox =x tak samo. Więc cosx ≥ 0

	1
To jest ciąg geometryczny i q=		cosx
	2

	1−qn		a1
Sn=a1		=
	1−q		1−q

	1   ( )cosx   2
1≥
	1   1−( )cosx   2

	1		1
1−(		)cosx≥(		)cosx
	2		2

	1		1
(		)1≥(		)cosx
	2		2

1≤cosx cosx =1 x=2k*pi Co o tym myślicie ?