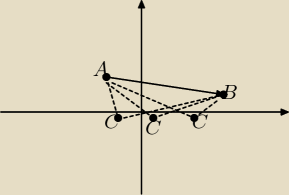
 jak widać z rysunku jest wiele możliwości ,gdzie leży punky C .
h − wysokość trójkąta i równocześnie odległość punktu C od prostej AB
należy wyjść ze wzoru na pole : P = 12 * |AB| * h
|AB| = √(5+2)2+(1−2)2 = 5√2
10 = 12 * 5√2 * h
h = 2√2
równanie prostej AB
y −2 = 1−25+2*(x+2)
y−2 = −17(x+2)
y−2 = −17x − 27 / *7
7y − 14 = −x − 2
x + 7y −14+2=0
x+7y12 =0
A = 1, B = 7 , C = −12
teraz jak już wspomniałam, h to również odległość punktu C od prostej AB , więc korzystamy ze
wzoru na odległość pkt od prostej
jak widać z rysunku jest wiele możliwości ,gdzie leży punky C .
h − wysokość trójkąta i równocześnie odległość punktu C od prostej AB
należy wyjść ze wzoru na pole : P = 12 * |AB| * h
|AB| = √(5+2)2+(1−2)2 = 5√2
10 = 12 * 5√2 * h
h = 2√2
równanie prostej AB
y −2 = 1−25+2*(x+2)
y−2 = −17(x+2)
y−2 = −17x − 27 / *7
7y − 14 = −x − 2
x + 7y −14+2=0
x+7y12 =0
A = 1, B = 7 , C = −12
teraz jak już wspomniałam, h to również odległość punktu C od prostej AB , więc korzystamy ze
wzoru na odległość pkt od prostej
| |A * x0+B * y0 + C | | ||
h = | ||
| √A2 + B2 |
| |1*x + 7*0 −12 | | ||
2√2 = | ||
| √12+72 |
| |x−12| | ||
2√2 = | / * √50
| |
| √50 |