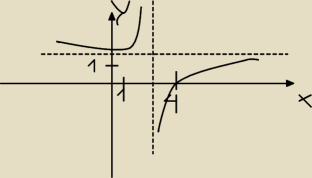
p Kamiska: na rysunku przedstawiono hiperbole. znajdz wzor funkcji ktorej wykresem jest ta hiperbola

aniabb: te asymptoty to mają dokładniejsze wartości

Kamiska: nie

krystek: To jak narysowałaś te przerywana linią , w których punktach przecinaja osie OX i OY?

aniabb: to tak pi razy drzwi

	−2
f(x)=		+ 2
	x−3

Kamiska: nie rozumiem tego zadania...

Artur_z_miasta_Neptuna: Kamiska −−− a czego konkretniej nie rozumiesz

Kamiska: tego calego zadania

Artur_z_miasta_Neptuna: masz rysunek pionowa przerywana linia pokazuje jaki 'x' nie należy do dziedziny ... (niech będzie że jest to

	a
x=3) wtedy wiesz, że funkcja będzie postaci y=		+ b ... bo dla niej wlaśnie 3 wypada
	x−3

z dziedziny. pozioma przerywana linia pokazuje jakiego 'y' ta funkcja nigdy nie przyjmie ... (niech będzie

	a
że jest to y = 2) wtedy wiesz, że funkcja będzie postaci y =		+2 ... bo ten ułamek
	x−3

nigdy nie będzie =0 ... więc zawsze y≠2 masz miejsce zerowe dla x=4, a więc podstawiasz:

	a
0 =		+ 2 ⇔ 0 = a + 2 ⇔ a=−2
	4−3

i stąd masz wzór funkcji

	−2
y=		+ 2
	x−3

koniec zadania rozjaśniłem troszeczkę

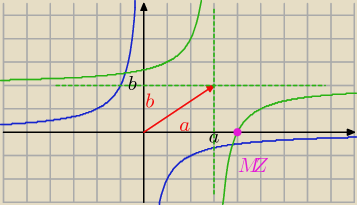
aniabb: hiperbola (asymptoty to osie ) rys niebieski

	c
f(x)=
	x

jeśli przesuniemy asymptoty rys zielony

	c
f(x)=		+b
	x−a

c obliczamy z miejsca zerowego MZ

	c
0 =		+b
	MZ−a

Kamiska:

Kamiska: o masakra. troche wyjasniles ale i tak ciezko...

Kamiska: to w sumie w rozwiazaniu zadania co musze napisac?

Artur_z_miasta_Neptuna: o boże ... jak zrozumiesz co chciemy Ci przekazać, to będziesz wiedziała.

Kamiska: przestan bozowac mi tu. chciales pomoc to pytam a nie chcesz to nie pisz. proste