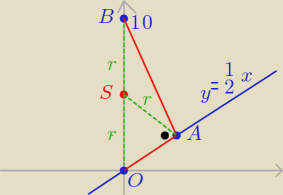
qq Misiek: Posił bym aby zrobić te zadanie albo o pomoc w zrobieniu. Nie pisząc mi bym skopiował z odpowiedzi maturalnych poniewarz nie będę wiedział skąd to się wzieło.. Z góry bardzo dziekuję.. Punkty B=(0,10) i O=(0,0) są wierzchołkami trójkąta prostokątnego OAB, w którym IKątOABI=90 Stopni. Przyprostokątna OA zawiera się w prostej o równaniu y= 1/2 x . Oblicz współrzędne punktu A i długośc przyprostokątnej OA

Eta: Witam Nie kopiuję rozwiązania, Rozwiązałabym tak: <OAB = 90^o IOBI = 10 −−− to długość przeciwprostokątnej tego trójkąta więc środek okręgu opisanego na trójkącie prostokątnym jest środkiem odcinka OB i r= ¹₂IOBI więc S( 0,5) a r = 5 rozwiązując układ równań tego okręgu i prostej OA otrzymasz współrzędne punktów O i A więc: (x−x_S)² + (y −y_S)² = r² x² + ( y −5)² = 25 i prosta y = ¹₂x zatem: x² +( ¹₂x −5)² = 25 x² +¹₄x² − 5x +25 =25 to: ⁵₄x² − 5x = 0 /*⁴₅ x² − 4x =0 => x= 0 lub x= 4 więc y= ¹₂*0 i y= ¹₂*4 to y=0 lub y= 2 więc punktami są ( 0,0) i ( 4,2) zatem skoro punkt B( 0,0) to punkt A( 4,2) policz IOAI ...... IOAI= p{(x_A − x_O)² + (y_A − y_O)²] odp: IOAI = 2√5 Sprawdzenie: IOAI= 2√5 IABI= 4√5 IOBI= 10 z tw. Pitagorasa: IOBI² = IOAI² + IOBI² 100= 4*5 + 16*5 100 = 100 więc wszystko gra

Eta: Oczywiście poprawiam chochlika IOAI=√(x_A −x_O)² + ( y_A −y_O)²

Eta: Miśku...... masz zatem, dwa rózne sposoby rozwiązania tego zadania odpowiada Ci .........

Misiek: Słuchajcie zrobiłem te zadanie sam i sprawdzicie mi czy ten sposób jest dobry Ponieważ inny od waszego,więc