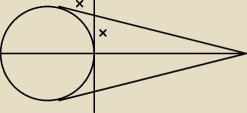
styczne name : Jak udowodnić że jeśli z punktu leżącego poza okręgiem poprowadzimy styczne do tego okręgu to odcinki wyznaczone przez punkt stycznosci są równe

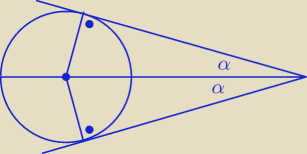
Godzio: Dwusieczna kąta przechodzi przez środek okręgu, myślę, że dalej sobie poradzisz

name: A co mam niby dalej zrobic? Bylbym wdzieczny za pomoc

PW: Nie poradził sobie. To są własności symetrii osiowej. Symetria osiowa jest izometrią, a więc przekształca prostą na prostą, okrąg na okrąg. Jeżeli w dodatku oś symetrii przechodzi przez środek okręgu, to przekształca ten okrąg "na siebie" (na ten sam okrąg). Popatrzmy teraz na sytuację na rysunku. Nie ma oznaczeń, więc powiedzmy tak: "górna" półprosta ma dokładnie jeden punkt wspólny Q z okręgiem (bo jest styczna). W symetrii osiowej o osi przechodzącej przez środek okręgu przekształca się na półprostą, która też ma dokładnie jeden punkt wspólny R z tym samym okręgiem − jest więc tą "dolną" styczną. Początek obu półprostych przekształca się na siebie. Obrazem odcinka PQ jest odcinek PR, a symetria osiowa jest izometrią, więc lPRl= lPQl.

Mila: Name, masz dwa trójkaty prostokątne przystające.

name: Dopiero pozniej zauwazylem ze te kropki to kat prosty. A zapomnialem ze styczna przeciez zawsze pod katem prostym. Ale i tak dzieki. Wiem to sa trojkaty podobne, zasada k,b,k a nawet przystajace/ Ale dzieki