Pomocy proszę Roki: Ściana boczna ostrosłupa prawidłowego trójkątnego jest trójkątem równoramiennym o wysokości h i kącie przy podstawie α.wyznacz objętość tego ostrosłupa

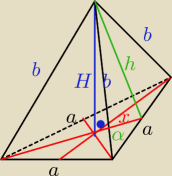
Basia: ściana boczna: trójkąt równoramienny

	a2
tgα=
	h

tgα=^a_2h a=2h*tgα podstawa: trójkąt równoboczny o boku a

	a√3
hp =
	2

	2h√3*tgα
hp =
	2

h_p = h√3*tgα x = ¹₃*h_p

	h√3*tgα
x=
	3

z tw.Pitagorasa x² + H² = h²

h2*3*tg2α
	+ H2 = h2
9

h2*tg2α
	+ H2 = h2
3

	h2*tg2α
H2 = h2 −
	3

	3−tg2α
H2 = h2*
	3

	√3−tg2α
H = h*
	√3

	a2√3		4h2*√3*tg2α
Pp =		=
	4		4

V = ¹₃*P_p*H

	4h2*√3*tg2α		√3−tg2α
V = 13*		*h*
	4		√3

	h3*tg2α*√3−tg2α
V =
	3

uprzedzam, że mogłam się gdzieś w rachunkach pomylić

Roki: ok narazie dzięki a jeszcze będę liczyć

Roki: Basiu czy możesz mi wytłumaczyć skąd te 3 3−tg2α H2 = h2* ____________ 3

Roki: Proszę o pomoc

Roki: pomocy błagam

Basia:

	h2*tg2α
H2 = h2 −
	3

wyłączamy h² przed nawias

	tg2α
H2 = h2(1−		)
	3

sprowadzamy do wspólnego mianownika

	3−tg2α
H2 = h2*
	3

Roki: ok dzięki ,a dalej tak jak wyżej?

Basia: Tak.

Roki: Dziękuje