Oblicz długości krawędzi prostopadłościanu. Romek01: Pole powierzchni całkowitej prostopadłościanu wynosi 50(1+2√3)cm². Przekątna jednej ze ścian bocznych jest nachylona do płaszczyzny podstawy pod kątem 45⁰, a przekątna sąsiedniej ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem 60⁰.

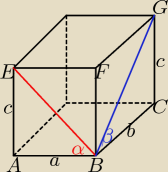
Basia: α=45 ⇒ tr.BAE jest prostokątny równoramienny ⇒ c=a β=60 ⇒ tr.BCG jest prostokątny z kątami 30 i 60 ⇒ c=b√3 c=a c=b√3 a=b√3 P_c = 2(ab+ac+bc) = 2(b²√3+3b²+b²√3) = 2b²(3+2√3) stąd 2b²(3+2√3) = 50(1+√3) wylicz b i resztę

Romek01: Wyniki: b=5√3 c=a=5 Dobre? Czy gdzieś machnąłem się w obliczeniach?