znajdź równania stycznych pooooo: Znajdź równania stycznych do okręgu o równaniu x2 + y2 = 4, przechodzących przez punkt P(4,−2).

Aga1.: Czy to miało być x²+y²=4?

pooooo: tak

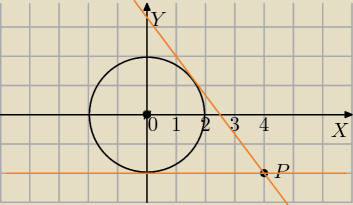
Mila: r=2 y=−2 to jedna styczna s: y=ax+b równanie stycznej −2=4a+b ⇔b=−2−4a s: y=ax−2−4a⇔ax−y−2−4a=0 (równanie ogólne) odległość p.(0;0) od prostej jest równa 2.

|a*0−0−2−4a|
	=2⇔
√a2+1

|2+4a|=2√a²+1⇔|1+2a|=√a²+1 1+4a+4a²=a²+1 3a²+4a=0

	4
a(3a+4)=0⇔a=0 lub a=−
	3

stąd

	4		4		10
y=−2 lub y=−		x+b⇔−2=−		*4+b⇔b=
	3		3		3

	4		10
y=−2 lub y=−		x+−
	3		3

Aga1.: Prosta z okręgiem ma jeden punkt wspólny, gdy odległość środka okręgu (0,0)od prostej y=a(x−4)−2 jest równa promieniowi r=2 Prosta w postaci ogólnej: ax−y−4a−2=0 Ze wzoru na odległość punktu od prostej oblicz a

Ia*0−0−4a−2I
	=2
√a2+1

Eta: Witam dziewczyny ładne rysunki